
【題目】已知函數![]() ,
,![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)若關于![]() 的方程
的方程![]() 有實數根,求實數
有實數根,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() ;(2)當
;(2)當![]() 時,方程
時,方程![]() 有實數根.
有實數根.
【解析】試題分析:(1)函數求導![]() ,從而得單調區間;
,從而得單調區間;
(2)方程![]() 有實數根,即函數
有實數根,即函數![]() 存在零點,分類討論函數
存在零點,分類討論函數![]() 的單調性,從而得有零點時參數的范圍.
的單調性,從而得有零點時參數的范圍.
試題解析:
(1)依題意,得![]()
![]() ,
,![]() .
.
令![]() ,即
,即![]() .
.
解得![]() ;
;
令![]() ,即
,即![]() .
.
解得![]() .
.
故函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]() .
.
(2)由題得,![]()
![]() .
.
依題意,方程![]() 有實數根,
有實數根,
即函數![]() 存在零點.
存在零點.
又![]() .
.
令![]() ,得
,得![]() .
.
當![]() 時,
時,![]() .
.
即函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
而![]() ,
,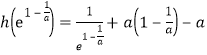
![]() .
.
所以函數![]() 存在零點;
存在零點;
當![]() 時,
時,![]() ,
,![]() 隨
隨![]() 的變化情況如下表:
的變化情況如下表:

所以![]() 為函數
為函數![]() 的極小值,也是最小值.
的極小值,也是最小值.
當![]() ,即
,即![]() 時,函數
時,函數![]() 沒有零點;
沒有零點;
當![]() ,即
,即![]() 時,注意到
時,注意到![]() ,
,
![]() ,
,
所以函數![]() 存在零點.
存在零點.
綜上所述,當![]() 時,方程
時,方程![]() 有實數根.
有實數根.


 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:
【題目】給定圓P:x2+y2=2x及拋物線S:y2=4x,過圓心P作直線l,此直線與上述兩曲線的四個交點,自上而下順次為A,B,C,D;如果線段AB,BC,CD的長度按此順序構成一個等差數列,則直線l的方程為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的三個內角分別為A,B,C,且A≠ ![]() .
.
(1)化簡 ![]() ;
;
(2)若角A滿足sinA+cosA= ![]() .
.
(i)試判斷△ABC是銳角三角形還是鈍角三角形,并說明理由;
(ii)求tanA的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司準備將1000萬元資金投入到市環保工程建設中,現有甲、乙兩個建設項目選擇,若投資甲項目一年后可獲得的利潤![]() (萬元)的概率分布列如下表所示:
(萬元)的概率分布列如下表所示:

且![]() 的期望
的期望![]() ;若投資乙項目一年后可獲得的利潤
;若投資乙項目一年后可獲得的利潤![]() (萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為
(萬元)與該項目建設材料的成本有關,在生產的過程中,公司將根據成本情況決定是否在第二和第三季度進行產品的價格調整,兩次調整相互獨立且調整的概率分別為![]() 和
和![]() .若乙項目產品價格一年內調整次數
.若乙項目產品價格一年內調整次數![]() (次數)與
(次數)與![]() 的關系如下表所示:
的關系如下表所示:

(1)求![]() 的值;
的值;
(2)求![]() 的分布列;
的分布列;
(3)若![]() ,則選擇投資乙項目,求此時
,則選擇投資乙項目,求此時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以下判斷正確的個數是( )
①相關系數![]() 值越小,變量之間的相關性越強.
值越小,變量之間的相關性越強.
②命題“存在![]() ”的否定是“不存在
”的否定是“不存在![]() ”.
”.
③“![]() ”為真是“
”為真是“![]() ”為假的必要不充分條件.
”為假的必要不充分條件.
④若回歸直線的斜率估計值是1.23,樣本點的中心為(4,5),則回歸直線方程是![]() .
.
A. 4 B. 2 C. 3 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如表資料:
日期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
晝夜溫差 | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數 | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗.
(1)求選取的2組數據恰好是相鄰兩個月的概率;
(2)若選取的是1月與6月的兩組數據,請根據3至5月份的數據,求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問(2)中所得線性回歸方程是否理想?
參考公式: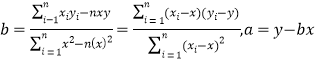 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x3+bx2+cx的極值點為x=﹣ ![]() 和x=1
和x=1
(1)求b,c的值與f(x)的單調區間
(2)當x∈[﹣1,2]時,不等式f(x)<m恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com