
【題目】如圖,一條小河岸邊有相距![]() 的
的![]() 兩個村莊(村莊視為岸邊上
兩個村莊(村莊視為岸邊上![]() 兩點),在小河另一側有一集鎮
兩點),在小河另一側有一集鎮![]() (集鎮視為點
(集鎮視為點![]() ),
),![]() 到岸邊的距離
到岸邊的距離![]() 為
為![]() ,河寬
,河寬![]() 為
為![]() ,通過測量可知,
,通過測量可知,![]() 與
與![]() 的正切值之比為
的正切值之比為![]() .當地政府為方便村民出行,擬在小河上建一座橋
.當地政府為方便村民出行,擬在小河上建一座橋![]() (
(![]() 分別為兩岸上的點,且
分別為兩岸上的點,且![]() 垂直河岸,
垂直河岸,![]() 在
在![]() 的左側),建橋要求:兩村所有人到集鎮所走距離之和最短,已知
的左側),建橋要求:兩村所有人到集鎮所走距離之和最短,已知![]() 兩村的人口數分別是
兩村的人口數分別是![]() 人、
人、![]() 人,假設一年中每人去集鎮的次數均為
人,假設一年中每人去集鎮的次數均為![]() 次.設
次.設![]() .(小河河岸視為兩條平行直線)
.(小河河岸視為兩條平行直線)

(1)記![]() 為一年中兩村所有人到集鎮所走距離之和,試用
為一年中兩村所有人到集鎮所走距離之和,試用![]() 表示
表示![]() ;
;
(2)試確定![]() 的余弦值,使得
的余弦值,使得![]() 最小,從而符合建橋要求.
最小,從而符合建橋要求.
 學業測評一課一測系列答案
學業測評一課一測系列答案科目:高中數學 來源: 題型:
【題目】一個透明密閉的正方體容器中,恰好盛有該容器一半容積的水,任意轉動這個正方體,則水面在容器中的形狀可以是:(1)三角形;(2)長方形;(3)正方形;(4)正六邊形.其中正確的結論是____________.(把你認為正確的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1所示,在梯形![]() 中,
中,![]() //
//![]() ,且
,且![]() ,
,![]() ,分別延長兩腰交于點
,分別延長兩腰交于點![]() ,點
,點![]() 為線段
為線段![]() 上的一點,將
上的一點,將![]() 沿
沿![]() 折起到
折起到![]() 的位置,使
的位置,使![]() ,如圖2所示.
,如圖2所示.
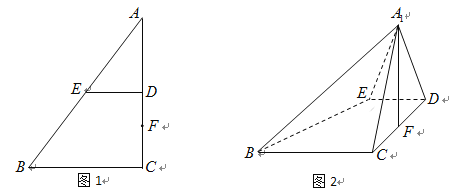
(1)求證:![]() ;
;
(2)若![]() ,
,![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() ,求四棱錐
,求四棱錐![]() 的表面積.
的表面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是橢圓
是橢圓![]() 上的兩點,已知向量
上的兩點,已知向量![]() ,
,![]() ,若
,若![]() 且橢圓的離心率
且橢圓的離心率![]() ,短軸長為2,
,短軸長為2,![]() 為坐標原點.
為坐標原點.
(1)求橢圓的方程;
(2)若直線![]() 過橢圓的焦點
過橢圓的焦點![]() (
(![]() 為半焦距),求直線
為半焦距),求直線![]() 的斜率
的斜率![]() 的值;
的值;
(3)試問:![]() 的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
的面積是否為定值?如果是,請給予證明;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]()
(1)當![]() ,
,![]() 時,求函數
時,求函數![]() 在
在![]() 上的最小值;
上的最小值;
(2)若函數![]() 在
在![]() 與
與![]() 處的切線互相垂直,求
處的切線互相垂直,求![]() 的取值范圍;
的取值范圍;
(3)設![]() ,若函數
,若函數![]() 有兩個極值點
有兩個極值點![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以
為參數),以![]() 為極點,
為極點,![]() 軸非負半軸為極軸建立極坐標系. 直線
軸非負半軸為極軸建立極坐標系. 直線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(Ⅰ)求圓![]() 的極坐標方程和直線的直角坐標方程;
的極坐標方程和直線的直角坐標方程;
(Ⅱ)射線![]() 與圓
與圓![]() 的交點為
的交點為![]() ,與直線
,與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“克拉茨猜想”又稱“![]() 猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數
猜想”,是德國數學家洛薩克拉茨在1950年世界數學家大會上公布的一個猜想:任給一個正整數![]() ,如果
,如果![]() 是偶數,就將它減半;如果
是偶數,就將它減半;如果![]() 為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數
為奇數就將它乘3加1,不斷重復這樣的運算,經過有限步后,最終都能夠得到1.己知正整數![]() 經過6次運算后得到1,則
經過6次運算后得到1,則![]() 的值為__________.
的值為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com