
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{8}$ | D. | $\frac{5π}{6}$ |
分析 利用函數y=Asin(ωx+φ)的圖象變換規律,三角函數的圖象的對稱性,求得m的最小值.
解答 解:將函數f(x)=$\sqrt{3}$sinx-cosx=2sin(x-$\frac{π}{6}$)的圖象向右平移m個單位(m>0),
可得y=2sin(x-m-$\frac{π}{6}$)的圖象,
若所得圖象對應的函數為偶函數,則-m-$\frac{π}{6}$=kπ+$\frac{π}{2}$,k∈Z,即m=-kπ-$\frac{2π}{3}$,
又m>0,
故當,k=-1時,m的最小值為$\frac{π}{3}$,
故選:A.
點評 本題主要考查函數y=Asin(ωx+φ)的圖象變換規律,正弦函數的圖象的對稱性,屬于基礎題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖,已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦點為F1,F2,P是橢圓上一點,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.則橢圓離心率e的取值范圍是( )
如圖,已知橢圓$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左右焦點為F1,F2,P是橢圓上一點,M在PF1上,$\overrightarrow{{F}_{1}M}$=2$\overrightarrow{MP}$,PO⊥F2M.則橢圓離心率e的取值范圍是( )| A. | $({0,\frac{{\sqrt{2}}}{2}})$ | B. | $({\frac{{\sqrt{2}}}{2},1})$ | C. | $({0,\frac{1}{2}})$ | D. | $({\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 某實心鋼質工件的三視圖如圖所示,其中側視圖為等腰三角形,俯視圖是一個半徑為3的半圓,現將該工件切削加工成一個球體,則該球體的最大體積為( )
某實心鋼質工件的三視圖如圖所示,其中側視圖為等腰三角形,俯視圖是一個半徑為3的半圓,現將該工件切削加工成一個球體,則該球體的最大體積為( )| A. | $\frac{4π}{3}$ | B. | $\frac{2π}{3}$ | C. | π | D. | $\frac{3π}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
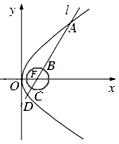 如圖,已知拋物線y2=4x的焦點為F,直線l過F且依次交拋物線及圓(x-1)2+y2=$\frac{1}{4}$于點A,B,C,D四點,則9|AB|+4|CD|的最小值為$\frac{37}{2}$.
如圖,已知拋物線y2=4x的焦點為F,直線l過F且依次交拋物線及圓(x-1)2+y2=$\frac{1}{4}$于點A,B,C,D四點,則9|AB|+4|CD|的最小值為$\frac{37}{2}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com