Question

13．已知△ABC是邊長為4的等邊三角形，P為平面ABC內一點，則$\overrightarrow{PA}•（\overrightarrow{PB}+\overrightarrow{PC}）$的最小值是（　　）

• A． -2
• B． $-\frac{3}{2}$
• C． -3
• D． -6 

Answer 1

分析 建立平面直角坐標系，表示出點的坐標，利用坐標法結合平面向量數量積的定義，求最小值即可．

解答 解：以BC中點為坐標原點，建立如圖所示的坐標系，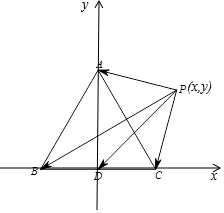

則A（0，2$\sqrt{3}$），B（-2，0），C（2，0），
設P（x，y），則$\overrightarrow{PA}$=（-x，2$\sqrt{3}$-y），
$\overrightarrow{PB}$=（-2-x，-y），
$\overrightarrow{PC}$=（2-x，-y），
所以$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）=-x•（-2x）+（2$\sqrt{3}$-y）•（-2y）
=2x²-4$\sqrt{3}$y+2y²
=2[x²+2（y-$\sqrt{3}$）²-3]；
所以當x=0，y=$\sqrt{3}$時，$\overrightarrow{PA}$•（$\overrightarrow{PB}$+$\overrightarrow{PC}$）取得最小值為2×（-3）=-6．
故選：D．

點評 本題主要考查了平面向量數量積的應用問題，根據條件建立坐標系，利用坐標法是解題的關鍵．