
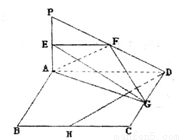
如圖所示,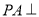 平面ABCD,四邊形ABCD為正方形,且
平面ABCD,四邊形ABCD為正方形,且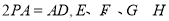 分別是線段PA、PD、CD、BC的中點.
分別是線段PA、PD、CD、BC的中點.
(1)求證:BC//平面EFG;
(2)求證: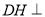 平面AEG;
平面AEG;
(3)求三棱錐E-AFG與四棱錐P-ABCD的體積比.
(1)因為BC∥AD,AD∥EF,所以BC∥EF.
因為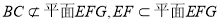 ,所以
,所以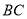 ∥平面EFG;
∥平面EFG;
(2)因為PA⊥平面ABCD,所以PA⊥DH ,即 AE⊥DH
因為△ADG≌△DCH ,所以∠HDC=∠DAG,∠AGD+∠DAG=90°,所以∠AGD+∠HDC=90°,所以DH⊥AG 又因為AE∩AG=A,所以DH⊥平面AEG;
(3)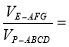
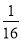 .
.
【解析】
試題分析:(1)首先利用平行公理即平行的傳遞性證明BC∥EF,再由已知條件并運用線面平行的判定,證明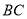 ∥平面EFG;(2)由已知PA⊥平面ABCD,可得PA⊥DH即證明了AE⊥DH,然后利用△ADG≌△DCH 得出對應角相等即∠HDC=∠DAG,∠AGD+∠DAG=90°即證明了DH⊥AG,從而由直線與平面的判定定理可證DH⊥平面AEG;(3)由三棱錐的等體積
∥平面EFG;(2)由已知PA⊥平面ABCD,可得PA⊥DH即證明了AE⊥DH,然后利用△ADG≌△DCH 得出對應角相等即∠HDC=∠DAG,∠AGD+∠DAG=90°即證明了DH⊥AG,從而由直線與平面的判定定理可證DH⊥平面AEG;(3)由三棱錐的等體積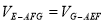 可得,
可得,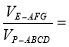
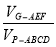 ,然后根據三棱錐和四棱錐的體積計算公式即可求出其體積比.
,然后根據三棱錐和四棱錐的體積計算公式即可求出其體積比.
試題解析:(1)因為BC∥AD,AD∥EF,所以BC∥EF.
因為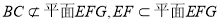 ,所以
,所以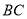 ∥平面EFG.
∥平面EFG.
(2)因為PA⊥平面ABCD,所以PA⊥DH ,即 AE⊥DH
因為△ADG≌△DCH ,所以∠HDC=∠DAG,∠AGD+∠DAG=90°,所以∠AGD+∠HDC=90°,所以DH⊥AG 又因為AE∩AG=A,所以DH⊥平面AEG.
(3)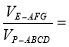
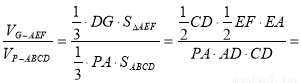
 .
.
考點:組合幾何體的面積、體積問題;直線與平面平行的判定;直線與平面垂直的判定.


科目:高中數學 來源: 題型:
| (a1+a2+…+an)π |
| 3 |
| A、z<y<x |
| B、x<z<y |
| C、x<y<z |
| D、y<z<x |
查看答案和解析>>
科目:高中數學 來源:2015屆山東師范大學附屬中學高三第一次模擬考試理科數學試卷(解析版) 題型:選擇題
某班班會準備從甲、乙等7名學生中選派4名學生發言,要求甲、乙兩人至少有一人參加,當甲乙同時參加時,他們兩人的發言不能相鄰,那么不同的發言順序的種數為
A.360 B.520 C.600 D.720
查看答案和解析>>
科目:高中數學 來源:2015屆山東師范大學附屬中學高三第一次模擬考試文科數學試卷(解析版) 題型:選擇題
已知兩個不同的平面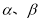 和兩個不重合的直線m、n,有下列四個命題:
和兩個不重合的直線m、n,有下列四個命題:
①若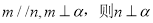 ; ②若
; ②若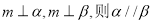 ;
;
③若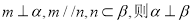 ; ④若
; ④若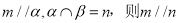 .
.
其中正確命題的個數是( )
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中數學 來源:2015屆安徽省皖南八校高三第一次聯考理科數學試卷(解析版) 題型:選擇題
在△ABC中,角A,B,C的對邊分別是a,b,c,若 ,則△ABC最小角的正弦值等于( )
,則△ABC最小角的正弦值等于( )
A.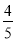 B.
B. 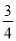 C.
C. D.
D.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com