
分析 由已知列式得到b,c與a的關系,把函數解析式用含有a的代數式表示.
(1)直接利用與正弦函數有關的復合函數的單調性求得f(x)的單調遞減區間;
(2)設sin(x+$\frac{π}{4}$)=t,則y=$\sqrt{2}$(1-a)t+a,由x得范圍得到t的范圍,然后對1-a>0、1-a=0、1-a<0分類討論求解得答案;
(3)由題意知a=8,則由mf(x)+nf(x-φ)=1得8(m+n)-7$\sqrt{2}$msin(x+$\frac{π}{4}$)-7$\sqrt{2}$nsin(x+$\frac{π}{4}$-φ)=1.令x+$\frac{π}{4}$=X,得8(m+n)-7$\sqrt{2}$(m+ncosφ)sinX+7$\sqrt{2}$nsinφcosX=1.
要使上式對任意X恒成立,則有$\left\{\begin{array}{l}{8(m+n)=1}\\{m+ncosφ=0}\\{nsinφ=0}\end{array}\right.$,由此求得答案.
解答 解:由題意可得,$\left\{\begin{array}{l}{f(0)=a+b=1}\\{f(\frac{π}{2})=a+c=1}\end{array}\right.$,則b=c=1-a,
∴f(x)=(1-a)(sinx+cosx)+a=$\sqrt{2}$(1-a)sin(x+$\frac{π}{4}$)+a.
(1)∵1-a=b>0,由2kπ+$\frac{π}{2}$<x+$\frac{π}{4}$<2kπ+$\frac{3π}{2}$,得:2kπ+$\frac{π}{4}$<x<2kπ+$\frac{5π}{4}$,
∴f(x)的遞減區間為[2kπ+$\frac{π}{4}$,2kπ+$\frac{5π}{4}$],k∈Z;
(2)設sin(x+$\frac{π}{4}$)=t,則y=$\sqrt{2}$(1-a)t+a,
∵$x∈(0,\frac{π}{2})$,
∴x+$\frac{π}{4}$∈($\frac{π}{4}$,$\frac{3π}{4}$),則t∈($\frac{\sqrt{2}}{2}$,1],
①當1-a>0時,f(x)∈(1,$\sqrt{2}$(1-a)t+a],此時|f(x)|≤2恒成立,
只需$\sqrt{2}$(1-a)t+a≤2,得a∈[-$\sqrt{2}$,1);
②當1-a=0時,f(x)=1,滿足題意;
②當1-a<0時,f(x)∈[$\sqrt{2}$(1-a)t+a,1),此時|f(x)|≤2恒成立,
只需$\sqrt{2}$(1-a)t+a≥-2,得a∈(1,4+3$\sqrt{2}$].
綜上所述,a的取值范圍為[-$\sqrt{2}$,4+3$\sqrt{2}$].
(3)可得a=8,則f(x)=8-7$\sqrt{2}$sin(x+$\frac{π}{4}$).
由mf(x)+nf(x-φ)=1得8(m+n)-7$\sqrt{2}$msin(x+$\frac{π}{4}$)-7$\sqrt{2}$nsin(x+$\frac{π}{4}$-φ)=1.
令x+$\frac{π}{4}$=X,得8(m+n)-7$\sqrt{2}$(m+ncosφ)sinX+7$\sqrt{2}$nsinφcosX=1.
要使上式對任意X恒成立,則有$\left\{\begin{array}{l}{8(m+n)=1}\\{m+ncosφ=0}\\{nsinφ=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{sinφ=0}\\{cosφ=1}\\{m=n=\frac{1}{16}}\end{array}\right.$.
所以m=$\frac{1}{16}$,n=$\frac{1}{16}$,φ=2kπ+π,k∈Z.
點評 本題考查三角函數值的恒等變換應用,考查y=Asin(ωx+φ)型函數的圖象和性質,訓練了函數恒成立問題的求解方法,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | $\frac{25}{3}$ | C. | -89 | D. | $\frac{17}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
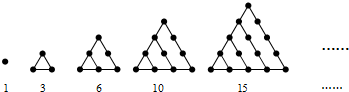
| A. | 35 | B. | 36 | C. | 45 | D. | 55 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
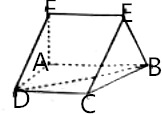 如圖,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通過直角梯形ABCD以直線AB為軸旋轉得到,且平面ABEF⊥平面ABCD
如圖,在直角梯形ABCD中,AB∥CD,∠DAB=90°,AD=CD=$\frac{1}{2}$AB=1,直角梯形ABEF可以通過直角梯形ABCD以直線AB為軸旋轉得到,且平面ABEF⊥平面ABCD查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | e3f(-14)<f(-5),e3f(-10)<f(-19) | B. | e3f(-14)>f(-5),e3f(-10)>f(-19) | ||
| C. | e3f(-14)<f(-5),e3f(-10)>f(-19) | D. | e3f(-14)>f(-4),e3f(-10)<f(-19) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,4] | B. | (-∞,2] | C. | [4,+∞) | D. | [2,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com