
分析 利用“1的飽和函數”的定義構造方程,判斷方程是否有解,可得結論.
解答 解:①f(x)=2x,D=R,則存在實數x0,使得2x0+1=2x0+2,解得x0=1,
因為此方程有實數解,
所以函數f(x)=2x是“1的飽和函數”.
②f(x)=$\frac{1}{x}$,D=(-∞,0)∪(0,+∞),
若f(x)=$\frac{1}{x}$是“1的飽和函數”,
則存在非零實數x0,使得$\frac{1}{{x}_{0}+1}$=$\frac{1}{{x}_{0}}$+1,
即x02+x0+1=0,
因為此方程無實數解,
所以函數f(x)=$\frac{1}{x}$不是“1的飽和函數”.
③f(x)=lg(x2+2),若存在x,使f(x+1)=f(x)+f(1)
則lg[(x+1)2+2]=lg(x2+2)+lg3
即2x2-2x+3=0,
∵△=4-24=-20<0,故方程無解.
即f(x)=lg(x2+2)不是“1的飽和函數”.
④f(x)=cosπx,存在x=$\frac{1}{3}$,使得f(x+1)=cos$\frac{4}{3}$π=-$\frac{1}{2}$=f(x)+f(1)=cos$\frac{1}{3}$π+cosπ=$\frac{1}{2}-1$,
即f(x)=cosπx是“1的飽和函數”.
故答案:①④
點評 本題考查“1的飽和函數”的判斷,是基礎題,解題時要注意函數的性質的合理運用.


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:高中數學 來源: 題型:解答題
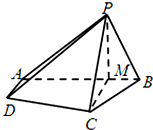 在四棱錐P-ABCD中,AD∥BC,∠ABC=∠APB=90°,點M是線段AB上的一點,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱錐P-ABCD中,AD∥BC,∠ABC=∠APB=90°,點M是線段AB上的一點,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$) | B. | $\sqrt{3}$f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{6}$) | D. | f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{6}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=$\frac{x}{2}$+$\frac{8}{x}$ | B. | y=sinx+$\frac{4}{sinx}$(0<x<π) | ||
| C. | y=ex+4e-x | D. | y=$\sqrt{{x}^{2}+1}$+$\frac{2}{\sqrt{{x}^{2}+1}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ①②③④ | B. | ①②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com