Question

19．向量$\overrightarrow a，\overrightarrow b，\overrightarrow c$滿足$|{\overrightarrow a}|=|{\overrightarrow b}|=1，\overrightarrow a•\overrightarrow b=-\frac{1}{2}，\left?{\overrightarrow a-\overrightarrow c，\overrightarrow b-\overrightarrow c}\right＞={60^0}$，則$\overrightarrow c$的模長的最大值為（　　）

• A． 2
• B． $\sqrt{3}$
• C． $\sqrt{2}$
• D． 1

Answer 1

分析 計算$\overrightarrow{a}，\overrightarrow{b}$的夾角，得出$\overrightarrow{a}，\overrightarrow{b}，\overrightarrow{c}$的起點和終點共圓，則外接圓的直徑即為|$\overrightarrow{c}$|的最大值．

解答 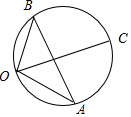解：設$\overrightarrow{OA}=\overrightarrow{a}$，$\overrightarrow{OB}=\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，
則OA=OB=1，
∵$\overrightarrow{a}•\overrightarrow{b}$=1×1×cos∠AOB=-$\frac{1}{2}$，∴∠AOB=120°，
∵＜$\overrightarrow{a}-\overrightarrow{c}$，$\overrightarrow{b}-\overrightarrow{c}$＞=∠BCA=60°，
∴O，A，B，C四點共圓，
設△AOB的外接圓半徑為r，則2r=$\frac{OA}{sin∠OBA}$=2，
∴OC的最大值為2r=2．
故選：A．

點評 本題考查了平面向量的基本定理，屬于中檔題．