
| A. | [-12,1] | B. | [-12,0] | C. | [-2,4] | D. | [1,4] |
分析 作出不等式組對應的平面區域,利用目標函數的幾何意義,結合直線的截距,利用數形結合進行求解即可.
解答 解:由z=x-3y得y=$\frac{1}{3}x-\frac{z}{3}$,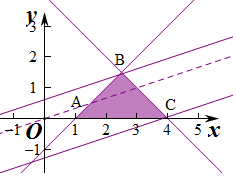
作出不等式組對應的平面區域如圖(陰影部分):
平移直線y=$\frac{1}{3}x-\frac{z}{3}$,
由圖象可知當直線y=$\frac{1}{3}x-\frac{z}{3}$經過點C(4,0)時,直線y=$\frac{1}{3}x-\frac{z}{3}$的截距最小,
此時z最大,此時z=4,
經過點B時,直線截距最大,此時z最小,
由$\left\{\begin{array}{l}{x-y=1}\\{x+y=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,即B($\frac{5}{2}$,$\frac{3}{2}$).
代入目標函數z=x-3y,
得z=$\frac{5}{2}$-3×$\frac{3}{2}$=-2,
即-2≤z≤4,
故選:C.
點評 本題主要考查線性規劃的基本應用,利用目標函數的幾何意義是解決問題的關鍵,利用數形結合是解決問題的基本方法.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
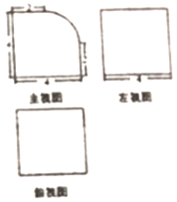
| A. | 64-4π | B. | 64+6π | C. | 48+4π | D. | 64-6π |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 已知在四棱錐C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是邊長為2的等邊三角形,AE=1,M為AB的中點.
已知在四棱錐C-ABDE中,DB⊥平面ABC,AE∥DB,△ABC是邊長為2的等邊三角形,AE=1,M為AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 57 | B. | 58 | C. | 62 | D. | 63 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | 4 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{10}$ | B. | 3 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 函數f(x)=Asin(ωx+φ)(A,ω,φ為常數,A>0,ω>0,0<φ<π)的圖象如圖所示,
函數f(x)=Asin(ωx+φ)(A,ω,φ為常數,A>0,ω>0,0<φ<π)的圖象如圖所示,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com