Question

14．橢圓x²+$\frac{{y}^{2}}{{b}^{2}}$=1（0＜b＜1）的左焦點為F，上頂點為A，右頂點為B，若△FAB的外接圓圓心P（m，n）在直線y=-x的左下方，則該橢圓離心率的取值范圍為（　　）

• A． （$\frac{\sqrt{2}}{2}$，1）
• B． （$\frac{1}{2}$，1）
• C． （0，$\frac{\sqrt{2}}{2}$）
• D． （0，$\frac{1}{2}$）

Answer 1

分析 方法一：分別求出線段FA與AB的垂直平分線方程，聯立解出圓心坐標P，利用m+n＜0，與離心率計算公式即可得出；
方法二：設△FAB的外接圓方程，將三點代入，即可求得P點坐標，由m+n＜0，求得b和c的關系，即可求得橢圓離心率的取值范圍．

解答 解：方法一：如圖所示，B是右頂點（1，0），上頂點A（0，b），左焦點F（$\sqrt{1-{b}^{2}}$，0），
線段FB的垂直平分線為：x=$\frac{1-\sqrt{1-{b}^{2}}}{2}$．
線段AB的中點（$\frac{1}{2}$，$\frac{b}{2}$）．
∵k_AB=-b．
∴線段AB的垂直平分線的斜率k=$\frac{1}{b}$．
∴線段AB的垂直平分線方程為：y-$\frac{b}{2}$=$\frac{1}{b}$（x-$\frac{1}{2}$），
把x=$\frac{1-\sqrt{1-{b}^{2}}}{2}$=m，代入上述方程可得：y=$\frac{{b}^{2}-\sqrt{1-{b}^{2}}}{2b}$=n．
由P（m，n）在直線y=-x的左下方，
則m+n＜0，
∴$\frac{1-\sqrt{1-{b}^{2}}}{2}$+$\frac{{b}^{2}-\sqrt{1-{b}^{2}}}{2b}$＜0．
化為：b＜$\sqrt{1-{b}^{2}}$，又0＜b＜1，
解得：0＜b＜$\frac{\sqrt{2}}{2}$．
∴e=$\frac{c}{a}$=c=$\sqrt{1-{b}^{2}}$∈（$\frac{\sqrt{2}}{2}$，1）．
∴橢圓離心率的取值范圍（$\frac{\sqrt{2}}{2}$，1）．
故選A．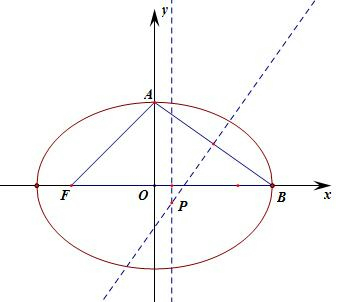

方法二：設A（0，b），B（a，0），F（-c，0），設△FAB的外接圓的方程x²+y²+Dx+Ey+F=0，
將A，B，F代入外接圓方程，解得：m=$\frac{-c+a}{2}$，n=$\frac{{b}^{2}-ac}{2b}$，
由P（m，n）在直線y=-x的左下方，
則m+n＜0，
∴$\frac{-c+a}{2}$+$\frac{{b}^{2}-ac}{2b}$＜0，整理得：1-c+b-$\frac{c}{b}$＜0，
∴b-c+$\frac{b-c}{b}$＜0，
∴b-c＜0，
由橢圓的離心率e=$\frac{c}{a}$=c，
∴2e²＞1，由0＜e＜1，
解得：$\frac{\sqrt{2}}{2}$＜e＜1，
∴橢圓離心率的取值范圍（$\frac{\sqrt{2}}{2}$，1）．
故選A．

點評 本題考查橢圓的簡單性質，三角形形外接圓求得求法，考查計算能力，數形結合思想，屬于中檔題．