
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
分析 ①根據特稱命題的否定是全稱命題進行判斷,
②根據否命題的定義進行判斷,
③根據逆否命題的等價性進行判斷.
解答 解:①“?x0∈R,x02-x0+1≤0”的否定是?x∈R,x2-x+1>0;∵判別式△=1-4=-3<0,∴?x∈R,x2-x+1>0恒成立,故①正確,
②“若x2+x-6≥0,則x>2”的否命題是“若x2+x-6<0,則x≤2”;由x2+x-6<0得-3<x<2,則x≤2成立,故②正確,
③命題“若x2-5x+6=0,則x=2”的逆否命題為假命題.
由x2-5x+6=0,則x=2或3,則原命題為假命題,則逆否命題也為假命題,故③錯誤,
故正確的命題是①②,
故選:C
點評 本題主要考查命題的真假判斷,涉及含有量詞的命題的否定,四種命題真假關系,比較基礎.


科目:高中數學 來源: 題型:解答題
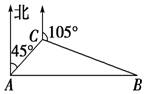 一商船行至索馬里海域時,遭到海盜的追擊,隨即發出求救信號.正在該海域執行護航任務的海軍“黃山”艦在A處獲悉后,即測出該商船在方位角為45°距離10海里的C處,并沿方位角為105°的方向,以9海里/時的速度航行.“黃山”艦立即以21海里/時的速度前去營救.如圖所示,求“黃山”艦靠近商船所需要的最少時間及所經過的路程.
一商船行至索馬里海域時,遭到海盜的追擊,隨即發出求救信號.正在該海域執行護航任務的海軍“黃山”艦在A處獲悉后,即測出該商船在方位角為45°距離10海里的C處,并沿方位角為105°的方向,以9海里/時的速度航行.“黃山”艦立即以21海里/時的速度前去營救.如圖所示,求“黃山”艦靠近商船所需要的最少時間及所經過的路程.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com