
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 時間代號t | 1 | 2 | 3 | 4 | 5 |
| 外來資金y(百億元) | 5 | 6 | 7 | 8 | 10 |
分析 (Ⅰ)由題意求得$\sum_{i=1}^{n}$(ti-$\overline{t}$)(yi-$\overline{y}$)=4.4+1.2+0+0.8+5.6=12,$\sum_{i=1}^{n}$(ti-$\overline{t}$)2=10,利用最小二乘法求得線性回歸方程的斜率和截距,即可求得y關于t的回歸直線方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$;
(Ⅱ)當x=6時,代入線性回歸方程,即可求得該地區2017年引進外來資金.
解答 解:(Ⅰ)由題意可知:
| 時間代號t | 1 | 2 | 3 | 4 | 5 |
| ti-$\overline{t}$ | -2 | -1 | 0 | 1 | 2 |
| (ti-$\overline{t}$)2 | 4 | 1 | 0 | 1 | 4 |
| 外來資金y(百億元) | 5 | 6 | 7 | 8 | 10 |
| yi-$\overline{y}$ | -2.2 | -1.2 | -0.2 | 0.8 | 2.8 |
| (ti-$\overline{t}$)(yi-$\overline{y}$)= | 4.4 | 1.2 | 0 | 0.8 | 5.6 |
點評 本題考查線性回歸方程的應用,考查利用最小二乘法求線性回歸方程的斜率和截距的方法,考查學生的計算能力,屬于中檔題.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | i | D. | -i |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
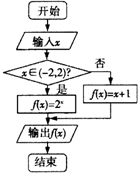
| A. | [0,log23] | B. | [-2,2] | C. | [0,log23]∪{2} | D. | [-2,log23]∪{2} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a>b>c | B. | c>a>b | C. | b>c>a | D. | c>b>a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 50 | B. | -7 | C. | -48 | D. | -49 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com