
分析 求函數的導數,判斷函數的取值情況,設m=f(x),利用換元法,將方程轉化為一元二次方程,利用根的分布建立條件關系即可得到結論.
解答 解:當x<0時,f′(x)=-ex-xex=-ex(x+1),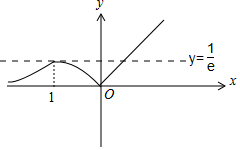
當x<-1時,f′(x)>0,
當-1≤x<0時,f′(x)≤0.
∴f(x)在(-∞,-1)上單調遞增,在(-1,0)單調遞減.
∴函數f(x)=-xex在(-∞,0)上有一個極大值為
f(-1)=$\frac{1}{e}$,作出函數f(x)的草圖如圖:
設m=f(x),當m>$\frac{1}{e}$時,方程m=f(x)有1個解,
當m=$\frac{1}{e}$時,方程m=f(x)有2個解,
當0<m<$\frac{1}{e}$時,方程m=f(x)有3個解,
當m=0時,方程m=f(x),有1個解,
當m<0時,方程m=f(x)有0個解,
則方程f2(x)+tf(x)+1=0等價為m2+tm+1=0,
要使關于x的方程f2(x)+tf(x)+1=0恰好有4個不相等的實數根,
等價為方程m2+tm+1=0有兩個不同的根m1>$\frac{1}{e}$且0<m2<$\frac{1}{e}$,
設g(m)=m2+tm+1,
則$\left\{\begin{array}{l}{g(0)=1>0}\\{g(\frac{1}{e})=\frac{1}{{e}^{2}}+\frac{t}{e}+1<0}\end{array}\right.$,即t<-e-$\frac{1}{e}$,
∴實數t的取值范圍為:$(-∞,-e-\frac{1}{e})$.
故答案為:$(-∞,-e-\frac{1}{e})$.
點評 本題考查了根的存在性及根的個數的判斷,考查了利用函數的導函數分析函數的單調性,考查了學生分析問題和解決問題的能力,利用換元法轉化為一元二次方程,是解決本題的關鍵,是中檔題.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
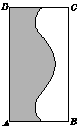 如圖,面積為4的矩形ABCD中有一個陰影部分,若往矩形ABCD中隨機投擲1000個點,落在矩形ABCD的非陰影部分中的點數為350個,試估計陰影部分的面積為( )
如圖,面積為4的矩形ABCD中有一個陰影部分,若往矩形ABCD中隨機投擲1000個點,落在矩形ABCD的非陰影部分中的點數為350個,試估計陰影部分的面積為( )| A. | 1.4 | B. | 1.6 | C. | 2.6 | D. | 2.4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
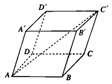 如圖,在平行六面體ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,則AC'=$\sqrt{69}$.
如圖,在平行六面體ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,則AC'=$\sqrt{69}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com