
| A. | 33 | B. | 32 | C. | 35 | D. | 34 |
分析 作出可行域,根據(jù)可行域,化簡目標(biāo)函數(shù),通過目標(biāo)函數(shù)幾何意義,根據(jù)直線的截距得出最優(yōu)解.
解答 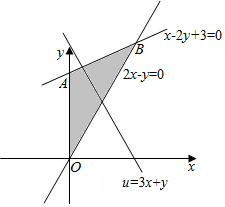 解:作出約束條件表示的可行域如圖:
解:作出約束條件表示的可行域如圖:
由z=8x•2y=23x+y可得u=3x+y得y=-3x+u.
由圖形可知當(dāng)直線y=-3x+u經(jīng)過B點時,直線的截距最大,
即z最大.
解方程組$\left\{\begin{array}{l}{2x-y=0}\\{x-2y+3=0}\end{array}\right.$,得B(1,2).
∴u的最大值為u=3×1+2=5.
則z=8x•2y的最大值為32.
故選:B.
點評 本題考查了簡單的線性規(guī)劃,考查轉(zhuǎn)化思想的應(yīng)用,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | i | B. | -i | C. | 1 | D. | -1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (2,3) | B. | (2,4) | C. | (2,3] | D. | [2,3] |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $?{x_0}∈[{0,+∞}),{2^{x_0}}≥{x_0}^2$ | B. | $?{x_0}∈({-∞,0}),{2^{x_0}}≥{x_0}^2$ | ||
| C. | ?x∈(-∞,0),2x≥x2 | D. | ?x∈[0,+∞),2x<x2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
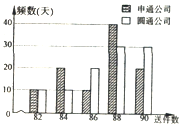 幾年來,網(wǎng)上購物風(fēng)靡,快遞業(yè)迅猛發(fā)展,某市的快遞業(yè)務(wù)主要由兩家快遞公司承接,即圓通公司與申通公司:“快遞員”的工資是“底薪+送件提成”:這兩家公司對“快遞員”的日工資方案為:圓通公司規(guī)定快遞員每天底薪為70元,每送件一次提成1元;申通公司規(guī)定快遞員每天底薪為120元,每日前83件沒有提成,超過83件部分每件提成10元,假設(shè)同一公司的快遞員每天送件數(shù)相同,現(xiàn)從這兩家公司各隨機抽取一名快遞員并記錄其100天的送件數(shù),得到如下條形圖:
幾年來,網(wǎng)上購物風(fēng)靡,快遞業(yè)迅猛發(fā)展,某市的快遞業(yè)務(wù)主要由兩家快遞公司承接,即圓通公司與申通公司:“快遞員”的工資是“底薪+送件提成”:這兩家公司對“快遞員”的日工資方案為:圓通公司規(guī)定快遞員每天底薪為70元,每送件一次提成1元;申通公司規(guī)定快遞員每天底薪為120元,每日前83件沒有提成,超過83件部分每件提成10元,假設(shè)同一公司的快遞員每天送件數(shù)相同,現(xiàn)從這兩家公司各隨機抽取一名快遞員并記錄其100天的送件數(shù),得到如下條形圖:查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{2}$ | D. | 8 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com