
| A. | 1 | B. | 4 | C. | 7 | D. | 16 |
分析 構造函數g(x)=f(x)-10x,則1,2,3為方程f(x)-10x=0的三個根,可設方程f(x)-10x=0的另一根為m,則方程f(x)-10x=(x-1)(x-2)(x-3)(x-m),由此能求出$\frac{1}{4}$[f(4)+f(0)].
解答 解:∵f(x)=x4+ax3+bx2+cx+d,其中a、b、c、d為常數.
f(1)=10,f(2)=20,f(3)=30,
∴構造函數g(x)=f(x)-10x,則g(1)=g(2)=g(3)=0,
即1,2,3為方程f(x)-10x=0的三個根
∵方程f(x)-10x=0有四個根,
故可設方程f(x)-10x=0的另一根為m
則方程f(x)-10x=(x-1)(x-2)(x-3)(x-m)
∴f(x)=(x-1)(x-2)(x-3)(x-m)+10x
故$\frac{1}{4}$[f(4)+f(0)]=$\frac{1}{4}$[(4-1)(4-2)(4-3)(4-m)+40+(0-1)(0-2)(0-3)(0-m)+0]=16.
故選:D.
點評 本題考查函數值的求法,是中檔題,解題時要認真審題,注意構造法的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
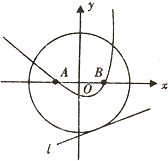 如圖,⊙O:x2+y2=16,A(-2,0),B(2,0)為兩個定點,l是⊙O的一條切線,若過A,B兩點的拋 物線以直線l為準線,則該拋物線的焦點的軌跡是( )
如圖,⊙O:x2+y2=16,A(-2,0),B(2,0)為兩個定點,l是⊙O的一條切線,若過A,B兩點的拋 物線以直線l為準線,則該拋物線的焦點的軌跡是( )| A. | 圓 | B. | 雙曲線 | C. | 橢圓 | D. | 拋物線 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|x>3或-3<x<0} | B. | {x|x<3或0<x<-3} | C. | {x|x<-3或x>3} | D. | {x|-3<x<0或0<x<3} |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com