
| 男 | 女 | 合計 | |
| 關注 | 60 | 20 | 80 |
| 不關注 | 20 | 20 | 40 |
| 合計 | 80 | 40 | 120 |
| p(k2≥k0) | 0.15 | 0.10 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)由抽樣比例求樣本中的數據;
(2)代入公式求出k2的值,查表得結論;
(3)確定所有的基本事件,用古典概型概率公式求值.
解答 解:(1)抽樣比為$\frac{8}{80}$=$\frac{1}{10}$,
則樣本中喜愛的觀從有60×$\frac{1}{10}$=6名;不喜愛的觀眾有8-6=2名.
(2)由已知數據可求得,k2=$\frac{120(60×20-20×20)^{2}}{80×40×80×40}$=7.5<10.828,
∴不能在犯錯誤的概率不超過0.010的前提下認為群眾性別與關注賽事有關.
(3)從(1)中的8名男性群眾中隨機選取2名進行跟蹤調查,共有方法${C}_{8}^{2}$=28,選到的兩名群眾中恰有一名觀注賽事,有6×2=12種,
故其概率為P=$\frac{12}{28}=\frac{3}{7}$.
點評 考查了抽樣的方法,獨立性檢驗及古典概型概率的求法,屬于基礎題.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案科目:高中數學 來源: 題型:選擇題
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}$ | B. | $\frac{96}{125}$ | C. | $\frac{32}{81}$ | D. | $\frac{100}{243}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
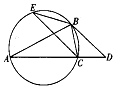 如圖,已知△ABC內接于圓,AB=AC,過點B作此圓的切線,與AC的延長線交于點D,且BD=2CD.
如圖,已知△ABC內接于圓,AB=AC,過點B作此圓的切線,與AC的延長線交于點D,且BD=2CD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,-2)∪(2,+∞) | B. | $[-2\sqrt{3},-2)∪(2,2\sqrt{3}]$ | C. | $[2,2\sqrt{3})$ | D. | [2,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若a≥b,則a2≥b2”的逆否命題為“若a2≤b2,則a≤b” | |
| B. | 命題“?x∈R,x2+x+1>0”的否定為“?x0∈R,x02+x0+1≤0” | |
| C. | 若p∧q為假命題,則p,q均為假命題 | |
| D. | “x=1”是“x2-3x+2=0”的必要不充分條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com