
分析 (1)由正弦定理可將acosC=2bcosA-ccosA轉(zhuǎn)化為sinAcosC+cosAsinC=2sinBcosA⇒sin(A+C)=sinB=2sinBcosA⇒cosA=$\frac{1}{2}$即可
(2)在△ABC中,由余弦定理得a2=b2+c2-2bc•cosA⇒8=(b-4)(b+2)=0,解得b=4,即可求得面積.
解答 解:(1)由正弦定理可將acosC=2bcosA-ccosA轉(zhuǎn)化為sinAcosC+cosAsinC=2sinBcosA,
⇒sin(A+C)=sinB=2sinBcosA⇒cosA=$\frac{1}{2}$
∵0<A<π∴A=$\frac{π}{3}$
(2)在△ABC中,由余弦定理得a2=b2+c2-2bc•cosA,即12=b2+4-2b→b2-2b
⇒8=(b-4)(b+2)=0,解得b=4,
s△ABC=$\frac{1}{2}bcsinA$=2$\sqrt{3}$
點(diǎn)評(píng) 本題考查了正余弦定理的應(yīng)用,屬于中檔題.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
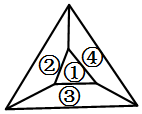 《數(shù)學(xué)萬(wàn)花筒》第7頁(yè)中談到了著名的“四色定理”.問題起源于1852年的倫敦大學(xué)學(xué)院畢業(yè)生弗朗西斯•加斯里.他給自己的弟弟弗萊德里克寫了一封信,信中提到了他認(rèn)為應(yīng)該很簡(jiǎn)單的一道小謎題.他一直嘗試著給一張英國(guó)各郡的地圖著色,在這個(gè)過程中,他發(fā)現(xiàn)使用四中顏色就可以實(shí)現(xiàn)他的目的,即使相鄰的兩個(gè)郡具有不同的顏色.“可以使用四種(或更少)顏色為平面上畫出的每張地圖著色,使任何相鄰的兩個(gè)地區(qū)的邊界線具有不同的顏色嗎?”他寫道.
《數(shù)學(xué)萬(wàn)花筒》第7頁(yè)中談到了著名的“四色定理”.問題起源于1852年的倫敦大學(xué)學(xué)院畢業(yè)生弗朗西斯•加斯里.他給自己的弟弟弗萊德里克寫了一封信,信中提到了他認(rèn)為應(yīng)該很簡(jiǎn)單的一道小謎題.他一直嘗試著給一張英國(guó)各郡的地圖著色,在這個(gè)過程中,他發(fā)現(xiàn)使用四中顏色就可以實(shí)現(xiàn)他的目的,即使相鄰的兩個(gè)郡具有不同的顏色.“可以使用四種(或更少)顏色為平面上畫出的每張地圖著色,使任何相鄰的兩個(gè)地區(qū)的邊界線具有不同的顏色嗎?”他寫道.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{1008}{1009}$ | B. | $-\frac{1009}{1008}$ | C. | 2017 | D. | $-\frac{1}{2017}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 三棱錐 | B. | 棱柱 | C. | 四棱臺(tái) | D. | 球 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com