
| A. | (0,1]∪[9,+∞) | B. | (0,$\sqrt{3}$]∪[9,+∞) | C. | (0,1]∪[4,+∞) | D. | (0,$\sqrt{3}$]∪[4,+∞) |
分析 分類討論,由要使橢圓C上存在點M滿足∠AMB=120°,∠AMB≥120°,∠AMO≥60°,當假設橢圓的焦點在x軸上,tan∠AMO=$\frac{\sqrt{3}}{\sqrt{m}}$≥tan60°,當即可求得橢圓的焦點在y軸上時,m>3,tan∠AMO=$\frac{\sqrt{m}}{\sqrt{3}}$≥tan60°=$\sqrt{3}$,即可求得m的取值范圍.
解答 解:假設橢圓的焦點在x軸上,則0<m<3時,
假設M位于短軸的端點時,∠AMB取最大值,要使橢圓C上存在點M滿足∠AMB=120°,
∠AMB≥120°,∠AMO≥60°,tan∠AMO=$\frac{\sqrt{3}}{\sqrt{m}}$≥tan60°=$\sqrt{3}$,
解得:0<m≤1;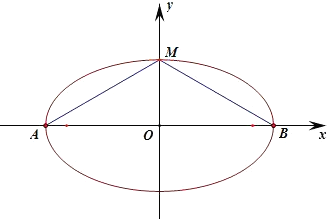
當橢圓的焦點在y軸上時,m>3,
假設M位于短軸的端點時,∠AMB取最大值,要使橢圓C上存在點M滿足∠AMB=120°,
∠AMB≥120°,∠AMO≥60°,tan∠AMO=$\frac{\sqrt{m}}{\sqrt{3}}$≥tan60°=$\sqrt{3}$,解得:m≥9,
∴m的取值范圍是(0,1]∪[9,+∞)
故選A.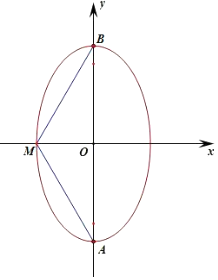
點評 本題考查橢圓的標準方程,特殊角的三角函數值,考查分類討論思想及數形結合思想的應用,考查計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 總體中的個體數不多時宜用簡單隨機抽樣 | |
| B. | 系統抽樣過程中,在總體均分后的每一部分中抽取一個個體,得到所需樣本 | |
| C. | 百貨商場的抓獎活動是抽簽法 | |
| D. | 整個抽樣過程中,每個個體被抽取的概率相等(有剔除時例外) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 在平面直角坐標系xOy中,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓C截直線y=1所得線段的長度為2$\sqrt{2}$.
在平面直角坐標系xOy中,已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的離心率為$\frac{\sqrt{2}}{2}$,橢圓C截直線y=1所得線段的長度為2$\sqrt{2}$.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)的一個周期為-2π | B. | y=f(x)的圖象關于直線x=$\frac{8π}{3}$對稱 | ||
| C. | f(x+π)的一個零點為x=$\frac{π}{6}$ | D. | f(x)在($\frac{π}{2}$,π)單調遞減 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
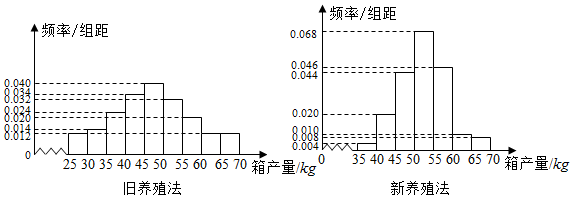
| 箱產量<50kg | 箱產量≥50kg | |
| 舊養殖法 | ||
| 新養殖法 |
| P(K2≥K) | 0.050 | 0.010 | 0.001 |
| K | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | -$\frac{7}{9}$ | B. | -$\frac{2}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com