
| A. | (-∞,1) | B. | (-∞,-1) | C. | (1,+∞) | D. | (-1,+∞) |
分析 復數(1-i)(a+i)=a+1+(1-a)i在復平面內對應的點在第二象限,可得$\left\{\begin{array}{l}{a+1<0}\\{1-a>0}\end{array}\right.$,解得a范圍.
解答 解:復數(1-i)(a+i)=a+1+(1-a)i在復平面內對應的點在第二象限,
∴$\left\{\begin{array}{l}{a+1<0}\\{1-a>0}\end{array}\right.$,解得a<-1.
則實數a的取值范圍是(-∞,-1).
故選:B.
點評 本題考查了復數的運算法則、幾何意義、不等式的解法,考查了推理能力與計算能力,屬于基礎題.


 學而優暑期銜接南京大學出版社系列答案
學而優暑期銜接南京大學出版社系列答案 Happy holiday歡樂假期暑假作業廣東人民出版社系列答案
Happy holiday歡樂假期暑假作業廣東人民出版社系列答案 快樂暑假暑假能力自測中西書局系列答案
快樂暑假暑假能力自測中西書局系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A∩B={x|x<$\frac{3}{2}$} | B. | A∩B=∅ | C. | A∪B={x|x<$\frac{3}{2}$} | D. | AUB=R |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | A∩B={x|x<0} | B. | A∪B=R | C. | A∪B={x|x>1} | D. | A∩B=∅ |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
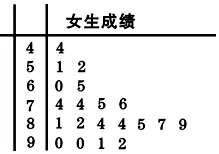 為了研究某學科成績(滿分100分)是否與學生性別有關,采用分層抽樣的方法,從高二年級抽取了30名男生和20名女生的該學科成績,得到如圖所示女生成績的莖葉圖.其中抽取的男生中有21人的成績在80分以下,規定80分以上為優秀(含80分).
為了研究某學科成績(滿分100分)是否與學生性別有關,采用分層抽樣的方法,從高二年級抽取了30名男生和20名女生的該學科成績,得到如圖所示女生成績的莖葉圖.其中抽取的男生中有21人的成績在80分以下,規定80分以上為優秀(含80分).| 優秀 | 非優秀 | 總計 | |
| 男生 | |||
| 女生 | |||
| 總計 | 50 |
| 參考數據 | 當x2≤2.706時,無充分證據判定變量A,B有關聯,可以認為兩變量無關聯; |
| 當x2>2.706時,有90%的把握判定變量A,B有關聯; | |
| 當x2>3.841時,有95%的把握判定變量A,B有關聯; | |
| 當x2>6.635時,有99%的把握判定變量A,B有關聯. |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (0,1]∪[9,+∞) | B. | (0,$\sqrt{3}$]∪[9,+∞) | C. | (0,1]∪[4,+∞) | D. | (0,$\sqrt{3}$]∪[4,+∞) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com