
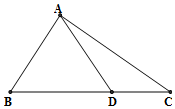
 如圖,在△ABC中,AB=2,3acosB-bcosC=ccosB,點D在線段BC上.
如圖,在△ABC中,AB=2,3acosB-bcosC=ccosB,點D在線段BC上.分析 (Ⅰ)由三角形內角和定理,兩角和的正弦函數公式,正弦定理化簡已知等式可得3sinAcosB=sinA,結合sinA>0,可求$cosB=\frac{1}{3}$,利用同角三角函數基本關系式可求sinB,進而可求$∠ADB=\frac{π}{4}$,由正弦定理即可求得AD的值.
(Ⅱ)設DC=a,則BD=2a,利用已知及三角形面積公式可求a,利用余弦定理可求AC,由正弦定理可得$sin∠CAD=\frac{{\sqrt{2}}}{4}sin∠ADC$,結合sin∠ADB=sin∠ADC,即可求值得解.
解答 (本小題滿分12分)
解:(Ⅰ)∵3acosB-bcosC=ccosB,
∴3sinAcosB=sinCcosB+sinBcosC,3sinAcosB=sin(B+C),
∵B+C=π-A,
∴3sinAcosB=sinA,
∵A∈(0,π),
∴sinA>0,$cosB=\frac{1}{3}$.…(2分)
∵B∈(0,π),
∴$sinB=\frac{{2\sqrt{2}}}{3}$.…(3分)
∵$∠ADC=\frac{3π}{4}$,
∴$∠ADB=\frac{π}{4}$,
在△ABD中,由正弦定理得,$\frac{AD}{sinB}=\frac{AB}{sin∠ADB}$,
∴$\frac{AD}{{\frac{{2\sqrt{2}}}{3}}}=\frac{2}{{\frac{{\sqrt{2}}}{2}}}$,$AD=\frac{8}{3}$.…(6分)
(Ⅱ)設DC=a,則BD=2a,
∵BD=2DC,△ACD的面積為$\frac{4}{3}\sqrt{2}$,
∴${S_{△ABC}}=3{S_{△ACD}}=4\sqrt{2}$,
∴$4\sqrt{2}=\frac{1}{2}×2×3a×\frac{{2\sqrt{2}}}{3}$,
∴a=2.…(8分)
∴$AC=\sqrt{4+36-2×2×6×\frac{1}{3}}=4\sqrt{2}$,由正弦定理可得$\frac{4}{sin∠BAD}=\frac{2}{sin∠ADB}$,
∴$sin∠BAD=\frac{1}{2}sin∠ADB$.$\frac{2}{sin∠CAD}=\frac{{4\sqrt{2}}}{sin∠ADC}$,
∴$sin∠CAD=\frac{{\sqrt{2}}}{4}sin∠ADC$,
∵sin∠ADB=sin∠ADC,
∴$\frac{sin∠BAD}{sin∠CAD}=\sqrt{2}$.…(12分)
點評 本題主要考查了三角形內角和定理,兩角和的正弦函數公式,正弦定理,同角三角函數基本關系式,三角形面積公式,余弦定理在解三角形中的綜合應用,考查了轉化思想,熟練掌握相關公式定理的應用是解題的關鍵,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
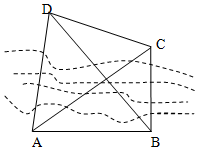 如圖,要測量河對岸C,D兩點間的距離,在河邊一側選定兩點A,B,測出AB的距離為20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.則C,D兩點之間的距離為10$\sqrt{10}$ m.
如圖,要測量河對岸C,D兩點間的距離,在河邊一側選定兩點A,B,測出AB的距離為20$\sqrt{3}$m,∠DAB=75°,∠CAB=30°,AB⊥BC,∠ABD=60°.則C,D兩點之間的距離為10$\sqrt{10}$ m.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com