
分析 (1)利用向量的數量積公式得到函數解析式,并化簡,得到函數周期;
(2)解不等式$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$得到x范圍即為所求.
解答 解:(1)f(x)=$\overrightarrow{a}$•$\overrightarrow{b}$+|$\overrightarrow{b}$|2,
$\begin{array}{l}f(x)=5\sqrt{3}cosxsinx+{sin^2}x+6{cos^2}x=\frac{{5\sqrt{3}}}{2}sin2x+\frac{1-cos2x}{2}+3(1+cos2x)\\=\frac{{5\sqrt{3}sin2x+5cos2x+7}}{2}=5sin(2x+\frac{π}{6})+\frac{7}{2}\end{array}$
∴$T=\frac{2π}{2}=π$.
(2)解:不等式$2kπ-\frac{π}{2}≤2x+\frac{π}{6}≤2kπ+\frac{π}{2}$得
∴$kπ-\frac{π}{3}≤x≤kπ+\frac{π}{6}$,f(x)單調遞增區間為$[{kπ-\frac{π}{3},kπ+\frac{π}{6}}]\;(k∈Z)$.
點評 本題考查了平面向量的運算以及三角函數式的化簡和正弦函數的性質運用;屬于中檔題.


 小學奪冠AB卷系列答案
小學奪冠AB卷系列答案科目:高中數學 來源: 題型:解答題
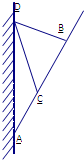 某固定在墻上的廣告金屬支架如圖所示,根據要求,AB長要超過4米(不含4米),C為AB的中點,B到D的距離比CD的長小1米,∠BCD=60°
某固定在墻上的廣告金屬支架如圖所示,根據要求,AB長要超過4米(不含4米),C為AB的中點,B到D的距離比CD的長小1米,∠BCD=60°查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{1}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B. | $\frac{x^2}{8}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | $\frac{x^2}{2}-{y^2}=1$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| x | … | 0 | 1 | 2 | 3 | 4 | … |
| y=x2-4x+3 | … | … |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com