
| A. | -$\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
分析 法一:由已知根據角的范圍,利用同角三角函數基本關系式可求sin(θ+$\frac{5π}{12}$)的值,由$\frac{π}{4}$-θ=(θ+$\frac{5π}{12}$)-$\frac{2π}{3}$,利用兩角差的余弦函數公式即可計算得解.
法二:由已知利用三角函數恒等變換的應用化簡可求2sin(2θ+$\frac{π}{3}$)=0,解得:θ=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,結合θ為銳角,可得:θ=$\frac{π}{3}$,進而利用兩角差的余弦函數公式及特殊角的三角函數值即可計算得解.
解答 解:法一:∵cos(θ+$\frac{5π}{12}$)=-$\frac{\sqrt{2}}{2}$,且θ為銳角,
∴θ+$\frac{5π}{12}$∈($\frac{5π}{12}$,$\frac{11π}{12}$),可得:sin(θ+$\frac{5π}{12}$)=$\sqrt{1-co{s}^{2}(θ+\frac{5π}{12})}$=$\frac{\sqrt{2}}{2}$,
∴cos($\frac{π}{4}$-θ)=cos[(θ+$\frac{5π}{12}$)-$\frac{2π}{3}$]=cos(θ+$\frac{5π}{12}$)cos$\frac{2π}{3}$+sin(θ+$\frac{5π}{12}$)sin$\frac{2π}{3}$=(-$\frac{\sqrt{2}}{2}$)×$(-\frac{1}{2})$+$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
法二:∵cos(θ+$\frac{5π}{12}$)=cos(θ+$\frac{π}{2}$-$\frac{π}{12}$)=-sin(θ-$\frac{π}{12}$)=-$\frac{\sqrt{2}}{2}$,
∴sin(θ-$\frac{π}{12}$)=$\frac{\sqrt{2}}{2}$,
∴sin(θ+$\frac{π}{4}$-$\frac{π}{3}$)=$\frac{1}{2}$sin(θ+$\frac{π}{4}$)-$\frac{\sqrt{3}}{2}$cos(θ+$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$,
∴化簡可得:sinθ(1+$\sqrt{3}$)+cosθ(1-$\sqrt{3}$)=2,兩邊平方可得:sin2θ+$\sqrt{3}$cos2θ=0,
∴可得:2sin(2θ+$\frac{π}{3}$)=0,解得:θ=$\frac{kπ}{2}$-$\frac{π}{6}$,k∈Z,
∵θ為銳角,可得:θ=$\frac{π}{3}$,
∴cos($\frac{π}{4}$-$\frac{π}{3}$)=cos$\frac{π}{4}$cos$\frac{π}{3}$+sin$\frac{π}{4}$sin$\frac{π}{3}$=$\frac{\sqrt{2}}{2}$×($\frac{1}{2}+\frac{\sqrt{3}}{2}$)=$\frac{\sqrt{2}+\sqrt{6}}{4}$.
故選:D.
點評 本題主要考查了三角函數恒等變換在三角函數化簡求值中的應用,考查了計算能力和轉化思想,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 7 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
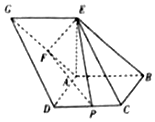 如圖,已知四邊形ABCD和ABEG均為平行四邊形,點E在平面ABCD內的射影恰好為點A,以BD為直徑的圓經過點A,C,AG的中點為F,CD的中點為P,且AD=AB=AE
如圖,已知四邊形ABCD和ABEG均為平行四邊形,點E在平面ABCD內的射影恰好為點A,以BD為直徑的圓經過點A,C,AG的中點為F,CD的中點為P,且AD=AB=AE查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
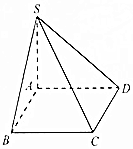 如圖,已知四棱錐S-ABCD的底面為矩形且SA⊥底面ABCD,若側棱SC=5$\sqrt{2}$,則此四棱錐的外接球表面積為( )
如圖,已知四棱錐S-ABCD的底面為矩形且SA⊥底面ABCD,若側棱SC=5$\sqrt{2}$,則此四棱錐的外接球表面積為( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com