
某中學高三年級從甲(文)、乙(理)兩個年級組各選出7名學生參加高校自主招生數學選拔考試,他們取得的成績(滿分100分)的莖葉圖如圖所示,其中甲組學生的平均分是85,乙組學生成績的中位數是83.
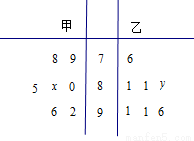
(1)求 和
和 的值;
的值;
(2)計算甲組7位學生成績的方差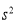 ;
;
(3)從成績在90分以上的學生中隨機抽取兩名學生,求甲組至少有一名學生的概率.
(1) ,
,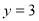 (2)40;(3)
(2)40;(3)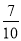 .
.
【解析】
試題分析:(1)利用平均數求出x的值,中位數求出y的值,解答即可.
(2)根據所給的莖葉圖,得出甲班7位學生成績,做出這7次成績的平均數,把7次成績和平均數代入方差的計算公式,求出這組數據的方差.
(3)設甲班至少有一名學生為事件A,其對立事件為從成績在90分以上的學生中隨機抽取兩名學生,甲班沒有一名學生;先計算出從成績在90分以上的學生中隨機抽取兩名學生的所有抽取方法總數,和沒有甲班一名學生的方法數目,先求出從成績在90分以上的學生中隨機抽取兩名學生,甲班沒有一名學生的概率,進而結合對立事件的概率性質求得答案.
試題解析:(1)∵甲組學生的平均分是85,
∴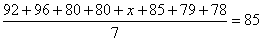 .
.
∴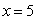 . 1分
. 1分
∵乙組學生成績的中位數是83,
∴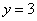 . 2分
. 2分
(2)甲組7位學生成績的方差為:
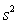
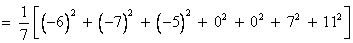
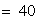 5分
5分
(3)甲組成績在90分以上的學生有兩名,分別記為 ,
,
乙組成績在90分以上的學生有三名,分別記為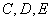 . 6分
. 6分
從這五名學生任意抽取兩名學生共有10種情況: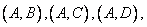
 . 9分
. 9分
其中甲組至少有一名學生共有7種情況:
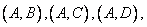
 . 11分
. 11分
記“從成績在90分以上的學生中隨機抽取兩名學生,甲組至少有一名學生”為事件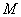 ,
,
則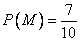 . 12分
. 12分
答:從成績在90分以上的學生中隨機抽取兩名學生,甲組至少有一名學生的概率為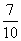 . 13分
. 13分
考點:1.古典概型及其概率計算公式;2.莖葉圖;3.極差、方差與標準差.


科目:高中數學 來源:2015屆江蘇省連云港高二下學期期末數學試卷(選修歷史)(解析版) 題型:解答題
已知函數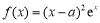 ,
,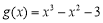 ,其中
,其中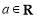 .
.
(1)當 時,求曲線
時,求曲線 在點
在點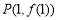 處的切線方程;
處的切線方程;
(2)若存在 ,使得
,使得 成立,求實數M的最大值;
成立,求實數M的最大值;
(3)若對任意的 ,都有
,都有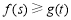 ,求實數
,求實數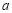 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com