
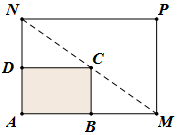
 如圖所示,某小區內有一矩形花壇,現將這一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B點在AM上,D點在AN上,且對角線MN過C點,已知AB=3米,AD=2米.
如圖所示,某小區內有一矩形花壇,現將這一矩形花壇ABCD擴建成一個更大的矩形花壇AMPN,要求B點在AM上,D點在AN上,且對角線MN過C點,已知AB=3米,AD=2米.分析 (1)由相似得到xy=6,即可用x,y表示z;
(Ⅱ)化簡矩形的面積,利用基本不等式,即可求得結論.
解答 解:(1)由相似得到$\frac{x}{3}=\frac{2}{y}$,∴xy=6…(2分)
∴面積z=(x+2)(y+3)…(4分)
(2)z=(x+2)(y+3)=(x+2)($\frac{6}{x}$+3)=3x+$\frac{12}{x}$+12≥24…(6分)
當且僅當3x=$\frac{12}{x}$,即x=2時,z有最小值24,
故DN的長為2米時,矩形AMPN的面積最小,最小值為24平方米…(8分)
點評 本題考查根據題設關系列出函數關系式,考查利用基本不等式求最值,解題的關鍵是確定矩形的面積.


科目:高中數學 來源: 題型:選擇題
| A. | 2016 | B. | -2016 | C. | 1008 | D. | -1008 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
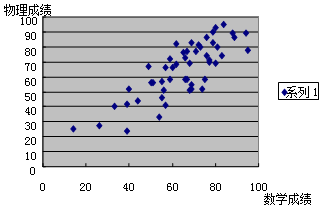 在調查分析某班級數學成績與物理成績的相關關系時,對數據進行統計分析得到如下散點圖,用回歸直線$\hat y=bx+a$近似刻畫其關系,根據圖形,b的數值最有可能是( )
在調查分析某班級數學成績與物理成績的相關關系時,對數據進行統計分析得到如下散點圖,用回歸直線$\hat y=bx+a$近似刻畫其關系,根據圖形,b的數值最有可能是( )| A. | 0 | B. | 1.55 | C. | 0.45 | D. | -0.24 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.
如圖,在梯形ABCD中,AB∥CD,AD=DC=CB=1,∠BCD=120°,四邊形BFED是以BD為直角腰的直角梯形,DE=2BF=2,平面BFED⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 200 | B. | 180 | C. | 150 | D. | 280 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com