
分析 (Ⅰ)根據函數$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x,x≥0}\\{-3x,x<0}\end{array}}\right.$的解析式,可得函數的圖象;數形結合,可得函數的單調遞減區間;
(Ⅱ)數形結合,對a進行分類討論,可得x∈[0,a]時f(x)的最大值的表達式.
解答 解:(Ⅰ)函數$f(x)=\left\{{\begin{array}{l}{-{x^2}+2x,x≥0}\\{-3x,x<0}\end{array}}\right.$的圖象如下圖所示: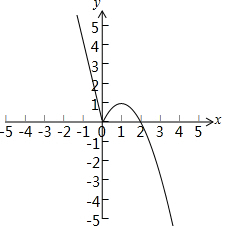
由圖可得:函數的單調遞減區間為(-∞,0]和[1,+∞);
(Ⅱ)若x∈[0,a],
當a∈(0,1)時,f(x)max=-a2+2a,
當a∈[1,+∞)時,f(x)max=1,
綜上可得:f(x)max=$\left\{\begin{array}{l}-{a}^{2}+2a,0<a<1\\ 1,a≥1\end{array}\right.$.
點評 本題考查的知識點是分段函數的應用,數形結合思想,函數的單調區間與最值,難度中檔.


 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| 品種 | 第一年 | 第二年 | 第三年 | 第四年 | 第五年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
| A. | 甲與乙穩定性相同 | |
| B. | 甲穩定性好于乙的穩定性 | |
| C. | 乙穩定性好于甲的穩定性 | |
| D. | 甲與乙穩定性隨著某些因素的變化而變化 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 0個 | B. | 1個 | C. | 2個 | D. | 3個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
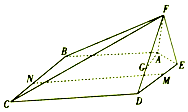 如圖,在五棱錐F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如圖,在五棱錐F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com