Question

18．已知圓C₁：（x-2）²+（y-3）²=1，圓C₂：（x-3）²+（y-4）²=9，動點P在x軸上，動點M，N分別在圓C₁和圓C₂上，則|PM|+|PN|的最小值是5$\sqrt{2}$-4．

Answer 1

分析 根據題意畫出圖形，結合圖形，求出圓C₁關于x軸的對稱圓的圓心坐標A與半徑，再求出圓A與圓C₂的圓心距減去兩個圓的半徑和，即為|PM|+|PN|的最小值．

解答 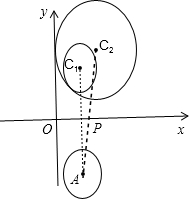解：如圖所示，
圓C₁關于x軸的對稱圓的圓心坐標A（2，-3），半徑為1，
圓C₂的圓心坐標C₂（3，4），半徑為3，
|PM|+|PN|的最小值為圓A與圓C₂的圓心距減去兩個圓的半徑和，
即為$\sqrt{（3-2）^{2}+（4+3）^{2}}$-4=5$\sqrt{2}$-4．
故答案為：5$\sqrt{2}$-4．

點評 本題考查圓的對稱圓方程以及兩圓的位置關系，兩點距離公式的應用問題，也考查了轉化思想與計算能力，數形結合思想的應用問題，是綜合性題目．