
 如圖,在多面體ABCDEF中,正三角形BCE所在平面與菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.
如圖,在多面體ABCDEF中,正三角形BCE所在平面與菱形ABCD所在的平面垂直,FD⊥平面ABCD,且$BC=4,FD=2\sqrt{3}$.分析 (1)過點E作EH⊥BC于點H,連接HD,推導出平面ABCD⊥平面BCE,從而平面EF∥平面ABCD.
(2)連接AC,HA,推導出HA⊥BC,以H為坐標原點,HB,HA,HE所在直線分別為x軸,y軸,z軸建立空間直角坐標系,利用向量法能求出二面角A-FB-E的余弦值.
解答 解:(1)直線EF與平面ABCD平行,理由如下:
如圖,過點E作EH⊥BC于點H,連接HD,因為在正三角形BCE中,BC=4,所以$EH=2\sqrt{3}$,
因為平面ABCD⊥平面BCE,EH?平面ABCD,
故平面EF∥平面ABCD.
(2)如圖,連接AC,HA,由(1)可得H為BC的中點,
又∠CBA=60°,故△ABC為等邊三角形,
所以HA⊥BC.
又EH⊥平面ABCD,故HB,HA,HE兩兩垂直,以H為坐標原點,
HB,HA,HE所在直線分別為x軸,y軸,z軸建立如圖所示的空間直角坐標系.
則$B(2,0,0),F(-4,2\sqrt{3},2\sqrt{3}),E(0,0,2\sqrt{3}),A(0,2\sqrt{3},0)$,
所以$\overrightarrow{BF}=(-6,2\sqrt{3},2\sqrt{3}),\overrightarrow{BA}=(-2,2\sqrt{3},0),\overrightarrow{BE}=(-2,0,2\sqrt{3})$,
設平面BEF的法向量為$\overrightarrow{n_1}=({x_1},{y_1},{z_1})$,
則$\left\{\begin{array}{l}{n_1}•\overrightarrow{BF}=0\\{n_1}•\overrightarrow{BE}=0\end{array}\right.$,即$\left\{\begin{array}{l}-6{x_1}+2\sqrt{3}{y_1}+2\sqrt{3}{z_1}=0\\-2{x_1}+2\sqrt{3}{z_1}=0\end{array}\right.$,
取z1=1,則$\overrightarrow{n_1}=(\sqrt{3},2,1)$是平面BEF的一個法向量,
設平面ABF的法向量為$\overrightarrow{n_2}=({x_2},{y_2},{z_2})$,
則$\left\{\begin{array}{l}{n_2}•\overrightarrow{BF}=0\\{n_2}•\overrightarrow{BE}=0\end{array}\right.$,即$\left\{\begin{array}{l}-6{x_2}+2\sqrt{3}{y_2}+2\sqrt{3}{z_2}=0\\-2{x_2}+2\sqrt{3}{y_2}=0\end{array}\right.$,
取y2=1,得$\overrightarrow{n_2}=(\sqrt{3},1,2)$是平面ABF的一個法向量.
所以$cos\left?{\overrightarrow{n_1},\overrightarrow{n_2}}\right>=\frac{{\overrightarrow{n_1}•\overrightarrow{n_2}}}{{|{\overrightarrow{n_1}}|•|{\overrightarrow{n_2}}|}}=\frac{3+2+2}{{\sqrt{8}×\sqrt{8}}}=\frac{7}{8}$,
由圖可知二面角A-FB-E為鈍角,故二面角A-FB-E的余弦值是$-\frac{7}{8}$.
點評 本題考查線面平行的證明,考查二面角的余弦值的求法,考查推理論證能力、運算求解能力、空間想象能力,考查數形結合思想、化歸與轉化思想、函數與方程思想,考查創新意識、應用意識,是中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
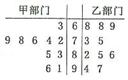 渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.
渝州集團對所有員工進行了職業技能測試從甲、乙兩部門中各任選10名員工的測試成績(單位:分)數據的莖葉圖如圖所示.| 分數 | [60,70) | [70,80) | [80,90) | [90,100] |
| 獎金 | a | 2a | 3a | 4a |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | -i | D. | i |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com