
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 ①不正確,例如取a=1,b=-2;
②取f(x)=x3,則f′(x)=3x2≥0,因此函數f(x)在R上單調遞增,即可判斷出正誤;
③不正確,例如取a=1,b=-2;
④“a>b”與“ac2≤bc2”互不推出,即可判斷出結論.
解答 解:①“a>b”是“a2>b2”的充要條件,不正確,例如取a=1,b=-2;
②取f(x)=x3,則f′(x)=3x2≥0,因此函數f(x)在R上單調遞增,∴“a>b”是“a3>b3”的充要條件,正確;
③“a>b”是“|a|>|b|”的充分條件,不正確,例如取a=1,b=-2;
④“a>b”與“ac2≤bc2”互不推出,因此不正確.
綜上只有:②.
故選:C.
點評 本題考查了不等式的性質與解法、函數的單調性,考查了推理能力與計算能力,屬于基礎題.


 高效智能課時作業系列答案
高效智能課時作業系列答案 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案科目:高中數學 來源: 題型:選擇題
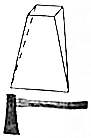 斧頭的形狀叫楔形,在《算數書》中又稱之為“鄆(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一線段.有一斧頭:上厚為三,下厚為六,高為五及袤(m$\stackrel{、}{a}$o)為二,問此斧頭的體積為幾何?意思就是說有一斧頭形的幾何體,上底為矩形,下底為一線段,上底的長為3,下底線段長為6,上下底間的距離(高)為5,上底矩形的寬為2,則此幾何體的體積是( )
斧頭的形狀叫楔形,在《算數書》中又稱之為“鄆(y$\stackrel{、}{u}$n)都”或“壍(qi$\stackrel{、}{a}$n)堵”:其上底是一矩形,下底是一線段.有一斧頭:上厚為三,下厚為六,高為五及袤(m$\stackrel{、}{a}$o)為二,問此斧頭的體積為幾何?意思就是說有一斧頭形的幾何體,上底為矩形,下底為一線段,上底的長為3,下底線段長為6,上下底間的距離(高)為5,上底矩形的寬為2,則此幾何體的體積是( )| A. | 6 | B. | 10 | C. | 16 | D. | 20 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\frac{{\sqrt{5}}}{2},+∞})$ | C. | $({1,\frac{5}{4}})$ | D. | $({\frac{5}{4},+∞})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
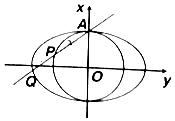 如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圓O:x2+y2=b2,過橢圓C的上頂點A的直線l:y=kx+b分別交圓O、橢圓C于不同的兩點P、Q,設$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.
如圖,橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圓O:x2+y2=b2,過橢圓C的上頂點A的直線l:y=kx+b分別交圓O、橢圓C于不同的兩點P、Q,設$\overrightarrow{AP}$=λ$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 如果α⊥β,那么α內一定存在直線平行于β | |
| B. | 如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ | |
| C. | 如果α不垂直于β,那么α內一定不存在直線垂直于β | |
| D. | 如果α⊥β,那么α內所有直線都垂直于β |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com