
| A. | $({1,\frac{{\sqrt{5}}}{2}})$ | B. | $({\frac{{\sqrt{5}}}{2},+∞})$ | C. | $({1,\frac{5}{4}})$ | D. | $({\frac{5}{4},+∞})$ |
分析 由于雙曲線的一條漸近線方程為:y=$\frac{b}{a}$x,及點(2,1)在“右”區域內,得出 $\frac{b}{a}$>$\frac{1}{2}$,從而得出雙曲線離心率e的取值范圍.
解答 解:雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一條漸近線方程為:y=$\frac{b}{a}$x,
∵點(2,1)在“右”區域內,
∴$\frac{b}{a}$×2>1,即$\frac{b}{a}$$>\frac{1}{2}$,
∴e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$>$\frac{\sqrt{5}}{2}$,
又e>1,
則雙曲線離心率e的取值范圍是($\frac{\sqrt{5}}{2}$,+∞).
故選:B.
點評 本小題主要考查雙曲線的簡單性質、不等式(組)與平面區域、不等式的性質等基礎知識,考查運算求解能力與轉化思想.屬于基礎題.


 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:高中數學 來源: 題型:選擇題
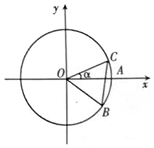 如圖,圓O與x軸的正半軸的交點為A,點C、B在圓O上,且點C位于第一象限,點B的坐標為($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,則$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值為( )
如圖,圓O與x軸的正半軸的交點為A,點C、B在圓O上,且點C位于第一象限,點B的坐標為($\frac{4}{5}$,-$\frac{3}{5}$),∠AOC=α,若|BC|=1,則$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值為( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{4}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{\sqrt{3}}{9}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com