
| 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
| 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
分析 (1)通過P(X=0)可求出P(X≥1)=1-P(X=0)=0.0408,利用二項分布的期望公式計算可得結(jié)論;
(2)(ⅰ)由(1)及知落在(μ-3σ,μ+3σ)之外為小概率事件可知該監(jiān)控生產(chǎn)過程方法合理;
(ⅱ)通過樣本平均數(shù)$\overline{x}$、樣本標(biāo)準(zhǔn)差s估計$\hat μ$、$\hat σ$可知($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)=(9.334,10.606),進而需剔除($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外的數(shù)據(jù)9.22,利用公式計算即得結(jié)論.
解答 解:(1)由題可知尺寸落在(μ-3σ,μ+3σ)之內(nèi)的概率為0.9974,
則落在(μ-3σ,μ+3σ)之外的概率為1-0.9974=0.0026,
因為P(X=0)=${C}_{16}^{0}$×(1-0.9974)0×0.997416≈0.9592,
所以P(X≥1)=1-P(X=0)=0.0408,
又因為X~B(16,0.0026),
所以E(X)=16×0.0026=0.0416;
(2)(ⅰ)如果生產(chǎn)狀態(tài)正常,一個零件尺寸在($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外的概率只有0.0026,一天內(nèi)抽取的16個零件中,出現(xiàn)尺寸在($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外的零件的概率只有0.0408,發(fā)生的概率很小.因此一旦發(fā)生這種狀況,就有理由認(rèn)為這條生產(chǎn)線在這一天的生產(chǎn)過程可能出現(xiàn)了異常情況,需對當(dāng)天的生產(chǎn)過程進行檢查,可見上述監(jiān)控生產(chǎn)過程的方法是合理的.
(ⅱ)由$\overline{x}$=9.97,s≈0.212,得μ的估計值為$\hat μ$=9.97,σ的估計值為$\hat σ$=0.212,由樣本數(shù)據(jù)可以看出一個
零件的尺寸在($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外,因此需對當(dāng)天的生產(chǎn)過程進行檢查.
剔除($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外的數(shù)據(jù)9.22,剩下的數(shù)據(jù)的平均數(shù)為
$\frac{1}{15}$(16×9.97-9.22)=10.02,
因此μ的估計值為10.02.
$\sum_{i=1}^{16}{x_i}$2=16×0.2122+16×9.972≈1591.134,
剔除($\hat μ$-3$\hat σ,\hat μ$+3$\hat σ$)之外的數(shù)據(jù)9.22,剩下的數(shù)據(jù)的樣本方差為
$\frac{1}{15}$(1591.134-9.222-15×10.022)≈0.008,
因此σ的估計值為$\sqrt{0.008}$≈0.09.
點評 本題考查正態(tài)分布,考查二項分布,考查方差、標(biāo)準(zhǔn)差,考查概率的計算,考查運算求解能力,注意解題方法的積累,屬于中檔題.


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
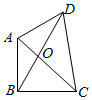 如圖,已知平面四邊形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC與BD交于點O,記I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,則( )
如圖,已知平面四邊形ABCD,AB⊥BC,AB=BC=AD=2,CD=3,AC與BD交于點O,記I1=$\overrightarrow{OA}$•$\overrightarrow{OB}$,I2=$\overrightarrow{OB}$•$\overrightarrow{OC}$,I3=$\overrightarrow{OC}$•$\overrightarrow{OD}$,則( )| A. | I1<I2<I3 | B. | I1<I3<I2 | C. | I3<I1<I2 | D. | I2<I1<I3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | (1,2) | B. | (1,2] | C. | (-2,1) | D. | [-2,1) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{5}{18}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{4}$=1 | B. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{8}$=1 | C. | $\frac{{x}^{2}}{4}-\frac{{y}^{2}}{8}$=1 | D. | $\frac{{x}^{2}}{8}-\frac{{y}^{2}}{4}$=1 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com