Question

5．已知點A（5，0），拋物線C：y²=2px（0＜p＜5）的準線為l，點P在C上，作PH⊥l于H，且|PH|=|PA|，∠APH=120°，則p=（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 由拋物線的定義可知：丨PH丨=x₁+$\frac{p}{2}$，根據三角形的性質，即可求得P點坐標，代入拋物線方程，即可求得p的值．

解答 解：設P（x₁，y₁），x₁＞0，過P點做PD⊥OA，
則由|PH|=|PA|，∠APH=120°，則∠APD=30°，
由拋物線的定義可知：丨PH丨=x₁+$\frac{p}{2}$，
∴|PA|=x₁+$\frac{p}{2}$，丨AD丨=5-x₁，
sin∠APD=$\frac{丨AD丨}{丨AP丨}$，則x₁=$\frac{10}{3}$-$\frac{p}{6}$，
則丨PD丨=丨AP丨cos∠APD=$\frac{\sqrt{3}}{2}$（$\frac{10}{3}$-$\frac{p}{6}$+$\frac{p}{2}$）=$\frac{\sqrt{3}}{2}$（$\frac{10}{3}$+$\frac{p}{3}$），
則P（$\frac{10}{3}$-$\frac{p}{6}$，$\frac{\sqrt{3}}{2}$（$\frac{10}{3}$+$\frac{p}{3}$），），將P代入拋物線方程，
整理得：p²-12p+20=0，解得：p=2，或p=10（舍去），
∴p的值2，
故選B．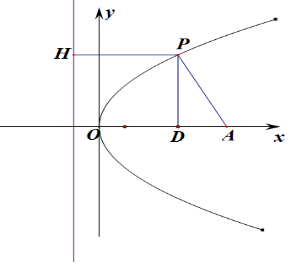

點評 本題考查拋物線的定義及簡單幾何性質，三角形的性質，考查數形結合思想，屬于中檔題．