
| A. | $\sqrt{6}π$ | B. | $4\sqrt{3}π$ | C. | $4\sqrt{2}π$ | D. | 6π |
分析 根據空間直線平面的垂直問題,得出棱錐的高,轉化頂點,補圖的正方體的外接球求解正三棱錐S-ABC的外接球的體積.
解答 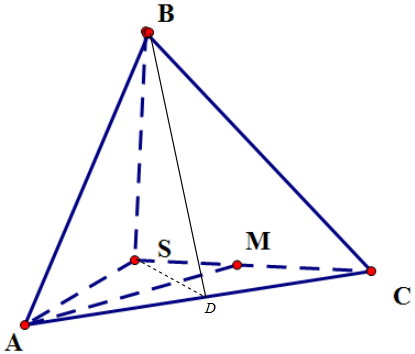 解:取AC中點D,則SD⊥AC,DB⊥AC,
解:取AC中點D,則SD⊥AC,DB⊥AC,
又∵SD⊥BD=D,∴AC⊥平面SDB,
∵SB?平面SBD,∴AC⊥SB,
又∵AM⊥SB,AM∩AC=A,
∴SB⊥平面SAC,
∴SA⊥SB,SC⊥SB,
根據對稱性可知SA⊥SC,從而可知SA,SB,SC兩兩垂直,
將其補為立方體,其棱長為2,其外接球即為立方體的外接球,半徑r=$\frac{\sqrt{3}}{2}×2=\sqrt{3}$,
∴正三棱錐S-ABC的外接球的體積=$\frac{4}{3}$π×3$\sqrt{3}$=4$\sqrt{3}$π.
故選:B.
點評 本題考查了空間空間幾何體的性質,學生的空間思維能力,計算能力,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
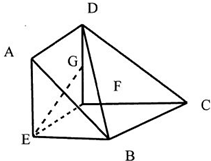 已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E為AB的中點,過E作EF∥AD,將四邊形AEFD沿EF折起使面AEFD⊥面EBCF.
已知直角梯形ABCD中,AD⊥AB,AB∥DC,AB=2,DC=3,E為AB的中點,過E作EF∥AD,將四邊形AEFD沿EF折起使面AEFD⊥面EBCF.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 5$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | $\frac{10\sqrt{6}}{3}$ | D. | 5$\sqrt{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-∞,2] | B. | [2,+∞) | C. | [2,$\frac{7}{2}$] | D. | [$\frac{7}{2}$,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
 中國傳統文化中很多內容體現了數學的對稱美,如圖所示的太極圖是由黑白兩個魚形紋組成的圓形圖案,充分展現了相互轉化、對稱統一的形式美、和諧美.給出定義:能夠將圓O的周長和面積同時平分的函數稱為這個圓的“優美函數”.給出下列命題:
中國傳統文化中很多內容體現了數學的對稱美,如圖所示的太極圖是由黑白兩個魚形紋組成的圓形圖案,充分展現了相互轉化、對稱統一的形式美、和諧美.給出定義:能夠將圓O的周長和面積同時平分的函數稱為這個圓的“優美函數”.給出下列命題:查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com