
分析 (1)求出f(x)的導(dǎo)數(shù),由題意可得切線的斜率,解a的方程可得a的值;
(2)求出f(x)的解析式,令g(x)=$\frac{f(x)}{x-1}$=$\frac{x+xlnx}{x-1}$,求得導(dǎo)數(shù),令h(x)=x-lnx-2(x>1),求出導(dǎo)數(shù),判斷單調(diào)性,運(yùn)用零點(diǎn)存在定理可得h(x)零點(diǎn)的范圍,進(jìn)而得到g(x)的單調(diào)性,即有g(shù)(x)的最小值,即可得證.
解答 解:(1)因?yàn)閒(x)=ax+xlnx,所以f′(x)=a+lnx+1.
因?yàn)楹瘮?shù)f(x)=ax+xlnx的圖象在點(diǎn)x=e處的切線斜率為3,
所以f′(e)=3,即a+lne+1=3.所以a=1.…(3分)
(2)證明:由(1)知,f(x)=x+xlnx,
令g(x)=$\frac{f(x)}{x-1}$=$\frac{x+xlnx}{x-1}$,
則g′(x)=$\frac{x-lnx-2}{(x-1)^{2}}$,-----------------------(5分)
令h(x)=x-lnx-2(x>1),
則h′(x)=1-$\frac{1}{x}$=$\frac{x-1}{x}$>0,
所以函數(shù)h(x)在(1,+∞)上單調(diào)遞增.…(7分)
因?yàn)閔(3)=1-ln3<0,h(4)=2-2ln2>0,
所以方程h(x)=0在(1,+∞)上存在唯一實(shí)根x0,且滿足x0∈(3,4).
當(dāng)1<x<x0,h(x)<0,即g′(x)<0,
當(dāng)x>x0時(shí),h(x)>0,即g′(x)>0,…(9分)
所以函數(shù)g(x)=$\frac{x+xlnx}{x-1}$在(1,x0)上單調(diào)遞減,在(x0,+∞)上單調(diào)遞增.
所以[g(x)]min=g(x0)=$\frac{{x}_{0}(1+ln{x}_{0})}{{x}_{0}-1}$=$\frac{{x}_{0}(1+{x}_{0}-2)}{{x}_{0}-1}$=x0.
因?yàn)閤0>3,所以x>1時(shí),令$\frac{f(x)}{x-1}$>3,即f(x)>3(x-1)…(12分)
點(diǎn)評(píng) 本題考查導(dǎo)數(shù)的運(yùn)用:求切線的斜率,注意運(yùn)用方程思想,考查不等式的證明,注意運(yùn)用構(gòu)造函數(shù)法,運(yùn)用導(dǎo)數(shù)判斷單調(diào)性以及函數(shù)零點(diǎn)存在定理的運(yùn)用,考查化簡整理的運(yùn)算能力,屬于中檔題.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0 | B. | 2 | C. | -2 | D. | 6 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
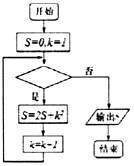
| A. | k≤2? | B. | k≤3? | C. | k≤4? | D. | k≤5? |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
| 分值區(qū)間 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 頻數(shù) | 20 | 40 | 80 | 50 | 10 |
| 分值區(qū)間 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 頻數(shù) | 45 | 75 | 90 | 60 | 30 |
| 女性用戶 | 男性用戶 | 合計(jì) | |
| “認(rèn)可”手機(jī) | 140 | 180 | 320 |
| “不認(rèn)可”手機(jī) | 60 | 120 | 180 |
| 合計(jì) | 200 | 300 | 500 |
| P(K2≧k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com