
| A. | [$\sqrt{5}$,2$\sqrt{2}$] | B. | [$\frac{1}{2}$,1] | C. | [$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$] | D. | [$\frac{\sqrt{2}}{2}$,$\sqrt{2}$] |
分析 由題意作出可行域,由向量的坐標加法運算求得$\overrightarrow{OA}$+$\overrightarrow{OM}$的坐標,把|$\overrightarrow{OA}$+$\overrightarrow{OM}$|轉化為可行域內的點M(x,y)到定點D(-1,0)的距離,數形結合可得答案.
解答 解:∵點A(1,0),點M(x,y),
∴$\overrightarrow{OA}$+$\overrightarrow{OM}$=(1+x,y),
設z=|$\overrightarrow{OA}$+$\overrightarrow{OM}$|=$\sqrt{(1+x)^{2}+{y}^{2}}$,
則z的幾何意義為M到定點D(-1,0)的距離,
由約束條件作平面區域如圖,
由圖象可知當M位于A(1,2)時,z取得最大值z=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
當M位于E時,z取得最小值z=$\frac{|-1+0-2|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$
即|$\overrightarrow{OA}$+$\overrightarrow{OM}$|的取值范圍是[$\frac{3\sqrt{2}}{2}$,2$\sqrt{2}$],
故選:C
點評 本題考查了簡單的線性規劃,考查了數形結合、轉化與化歸等解題思想方法,考查了向量模的求法,是中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
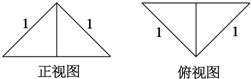 把邊長為1的正方形ABCD沿對角線BD折起,形成的三棱錐A-BCD的正視圖與俯視圖如圖所示,則其側視圖的面積為$\frac{1}{4}$,二面角B-AC-D的余弦值為$-\frac{1}{3}$.
把邊長為1的正方形ABCD沿對角線BD折起,形成的三棱錐A-BCD的正視圖與俯視圖如圖所示,則其側視圖的面積為$\frac{1}{4}$,二面角B-AC-D的余弦值為$-\frac{1}{3}$.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
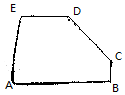 如圖所示的五邊形是由一個矩形截去一個角而得,且BC=1,DE=2,AE=3,AB=4,則$\overrightarrow{CD}$等于( )
如圖所示的五邊形是由一個矩形截去一個角而得,且BC=1,DE=2,AE=3,AB=4,則$\overrightarrow{CD}$等于( )| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | B. | $\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ | C. | -$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{2}{3}$$\overrightarrow{AE}$ | D. | -$\frac{1}{2}$$\overrightarrow{AB}$-$\frac{2}{3}$$\overrightarrow{AE}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ab>b2 | B. | $\frac{1}{a}$>$\frac{1}{b}$ | C. | $\frac{1}{a}$<$\frac{1}{b}$ | D. | a2>ab |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com