
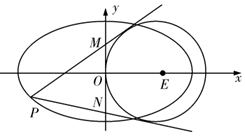
 已知橢圓C中心在原點,離心率$\frac{{\sqrt{2}}}{2}$,其右焦點是圓E:(x-1)2+y2=1的圓心.
已知橢圓C中心在原點,離心率$\frac{{\sqrt{2}}}{2}$,其右焦點是圓E:(x-1)2+y2=1的圓心.分析 (1)由已知條件分別求出a,c的值,而b2=a2-c2,代入求出橢圓的方程.
(2)假設存在點P滿足題意,設點P(x0,y0)(x0<0),M(0,m),N(0,n),利用條件求出直線PM方程,根據圓心E(1,0)到直線.的距離為1,求出m與點P坐標之間的關系,同理求出n與點P坐標之間的關系,利用韋達定理求出m+n,mn的表達式,算出|MN|,求出P點坐標.
解答 解:(1)設橢圓方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),半焦距為c,
因為橢圓的右焦點是圓E的圓心,則c=1,
因為橢圓的離心率為$\frac{\sqrt{2}}{2}$,則$\frac{c}{a}=\frac{\sqrt{2}}{2}$,即a=$\sqrt{2}c=\sqrt{2}$,
從而b2=a2-c2=1,
故橢圓C的方程為$\frac{{x}^{2}}{2}+{y}^{2}=1$.
(2)設點P(x0,y0)(x0<0),M(0,m),N(0,n),
則直線PM的方程為y=$\frac{{y}_{0}-m}{{x}_{0}}x+m$,即(y0-m)x-x0y+mx0=0,
因為圓心E(1,0)到直線PM的距離為1,
即$\frac{|{y}_{0}-m+{x}_{0}m|}{\sqrt{({y}_{\;}0-m)^{2}+{{x}_{0}}^{2}}}$=1,
即(y0-m)2+${{x}_{0}}^{2}$=(y0-m)2+2x0m(y0-m)+${{x}_{0}}^{2}{m}^{2}$,即(x0-2)m2+2y0m-x0=0,
同理(x0-2)n2+2y0n-x0=0.
由此可知,m,n為方程(x0-2)x2+2y0x-x0=0的兩個實根,
所以m+n=-$\frac{2{y}_{0}}{{x}_{0}-2}$,mn=-$\frac{{x}_{0}}{{x}_{0}-2}$,
|MN|=|m-n|=$\sqrt{(m+n)^{2}-4mn}$=$\sqrt{\frac{4{{y}_{0}}^{2}}{({x}_{0}-2)^{2}}+\frac{4{x}_{0}}{{x}_{0}-2}}$=$\sqrt{\frac{4{{x}_{0}}^{2}+4{{y}_{0}}^{2}-{x}_{0}}{({x}_{0}-2)^{2}}}$.
因為點P(x0,y0)在橢圓C上,則$\frac{{{x}_{0}}^{2}}{2}+{{y}_{0}}^{2}=1$,即${{y}_{0}}^{2}=1-\frac{{{x}_{0}}^{2}}{2}$,
則|MN|=$\sqrt{\frac{2{{x}_{0}}^{2}-8{x}_{0}+4}{({x}_{0}-2)^{2}}}$=$\sqrt{\frac{2({x}_{0}-2)^{2}-4}{({x}_{0}-2)^{2}}}$=$\sqrt{2-\frac{4}{({x}_{0}-2)^{2}}}$,
令$\sqrt{2-\frac{4}{({x}_{0}-2)^{2}}}$=$\frac{\sqrt{14}}{3}$,
則(x0-2)2=9,
因為x0<0,則x0=-1,${{y}_{0}}^{2}$=1-$\frac{{{x}_{0}}^{2}}{2}$=$\frac{1}{2}$,即${y}_{0}=±\frac{\sqrt{2}}{2}$,
故存在點P(-1,$±\frac{\sqrt{2}}{2}$)滿足題設條件.
點評 本題考查橢圓方程的求法,考查滿足條件的點的坐標的求法,是中檔題,解題時要認真審題,注意橢圓性質、韋達定理、直線與橢圓位置關系等知識點的合理運用.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 充分不必要條件 | B. | 必要不充分條件 | ||
| C. | 充要條件 | D. | 既不充分也不必要條件 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com