
分析 (Ⅰ)由題意可知:拋物線y2=8x的焦點為(2,0),c=2,即a2-b2=4,將($\sqrt{2}$,$\sqrt{3}$)代入橢圓方程,即可求得a和b的值,求得橢圓C方程;
已知橢圓C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一個焦點與拋物線y2=8x的焦點重合,點($\sqrt{2}$,$\sqrt{3}$)在C上
(Ⅱ)設直線l的方程為y=kx+b,代入橢圓方程,由韋達定理及中點坐標公式求得中點M坐標,根據斜率公式,直線OM的斜率為kOM=$\frac{{y}_{M}}{{x}_{M}}$=-$\frac{1}{2k}$,則kOM•k=-$\frac{1}{2}$,則OM的斜率與直線l的斜率的乘積為定值.
解答 解:(Ⅰ)拋物線y2=8x的焦點為(2,0),由題意可得:c=2,即a2-b2=4,
又點($\sqrt{2}$,$\sqrt{3}$)在橢圓C上,可得$\frac{2}{{a}^{2}}+\frac{3}{{b}^{2}}=1$,解得:a2=8,b2=4,
c2=a2-b2=4,
∴C的方程:$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1$;…(5分)
(Ⅱ)證明:設直線l的方程為y=kx+b(k,b≠0),A(x1,y1),B(x2,y2),…(6分)
$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,整理得:(1+2k2)x2+4kbx-2b2-8=0,
由韋達定理可知:x1+x2=-$\frac{4kb}{1+2{k}^{2}}$,…(8分)
即有AB的中點M的橫坐標為xM=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{2kb}{1+2{k}^{2}}$,縱坐標為yM=k(-$\frac{2kb}{1+2{k}^{2}}$)+b=$\frac{b}{1+2{k}^{2}}$,…(10分)
直線OM的斜率為kOM=$\frac{{y}_{M}}{{x}_{M}}$=-$\frac{1}{2k}$,即有kOM•k=-$\frac{1}{2}$,
故OM的斜率與直線l的斜率的乘積為定值.…(12分)
點評 本題考查拋物線與橢圓的標準方程及簡單幾何性質,考查直線與橢圓的位置關系,考查韋達定理及中點坐標公式的應用,考查計算能力,屬于中檔題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
 如圖為平面中兩個全等的直角三角形,將這兩個三角形繞著它們的對稱軸(虛線所在直線)旋轉一周得到一個幾何體,則該幾何體的體積為( )
如圖為平面中兩個全等的直角三角形,將這兩個三角形繞著它們的對稱軸(虛線所在直線)旋轉一周得到一個幾何體,則該幾何體的體積為( )| A. | 4π | B. | 8π | C. | 16π | D. | 32π |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\sqrt{2}$) | B. | ($\sqrt{2}$,2) | C. | ($\sqrt{2}$,-2) | D. | (4,2) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
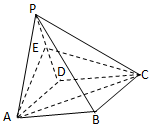 在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.
在四棱錐P-ABCD中,平面PAD⊥平面ABCD,∠APD=90°,PA=PD=AB=a,ABCD是矩形,E是PD的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{π}{9}$,0) | B. | ($\frac{π}{18}$,0) | C. | $(-\frac{π}{18},0)$ | D. | $(-\frac{5π}{18},0)$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com