
分析 由函數f(x-1)的圖象關于(1,0)對稱,且由y=f(x-1)向左平移1個單位可得y=f(x)的圖象可知,函數y=f(x)的圖象關于原點對稱,即函數y=f(x)為奇函數,由已知條件可得函數的周期為4,利用所求周期即可求解.
解答 解:∵函數f(x-1)的圖象關于(1,0)對稱
且把y=f(x-1)向左平移1個單位可得y=f(x)的圖象,
∴函數y=f(x)的圖象關于(0,0)對稱,即函數y=f(x)為奇函數,
∴f(0)=0,
∵f(x+2)=f(-x),又f(-x)=-f(x),
從而可得f(x+2)=-f(x),
將x換成x+2,可得f(x+4)=f(x),
即函數是以4為周期的周期函數,
∴f(2016)=f(504×4)=f(0)=0,
f(2017)=f(504×4+1)=f(1)=4,
f(2018)=f(504×4+2)=f(2)=-f(0)=0,
即有f(2016)+f(2017)+f(2018)=4.
故答案為:4.
點評 本題主要考出了函數的圖象的平移及函數圖象的對稱性的應用,利用賦值求解抽象函數的函數值,函數周期的求解是解答本題的關鍵所在.


科目:高中數學 來源: 題型:選擇題
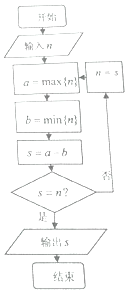 正整數的各數位上的數字重新排列后得到的最大數記為a=max{n},得到的最小數記為b=min{n}(如正整數n=2016,則a=6210,b=0126),執行如圖所,示的程序框圖,若輸入n=2017,則輸出的S的值為( )
正整數的各數位上的數字重新排列后得到的最大數記為a=max{n},得到的最小數記為b=min{n}(如正整數n=2016,則a=6210,b=0126),執行如圖所,示的程序框圖,若輸入n=2017,則輸出的S的值為( )| A. | 6174 | B. | 7083 | C. | 8341 | D. | 8352 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
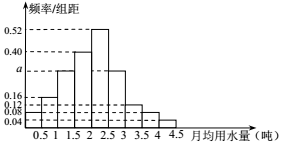 我國是世界上嚴重缺水的國家,城市缺水問題較為突出.某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準x(噸),用水量不超過 x 的部分按平價收費,超出 x 的部分按議價收費.為了了解全市居民用水量的分布情況,通過抽樣,獲得了 100 位居民某年的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.
我國是世界上嚴重缺水的國家,城市缺水問題較為突出.某市政府為了鼓勵居民節約用水,計劃在本市試行居民生活用水定額管理,即確定一個合理的居民月用水量標準x(噸),用水量不超過 x 的部分按平價收費,超出 x 的部分按議價收費.為了了解全市居民用水量的分布情況,通過抽樣,獲得了 100 位居民某年的月均用水量(單位:噸),將數據按照[0,0.5),[0.5,1),…,[4,4.5]分成9組,制成了如圖所示的頻率分布直方圖.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $[1,\frac{7}{4}]$ | B. | $[-\frac{7}{4},-1]$ | C. | $[-\sqrt{2},-1]$ | D. | $[-1,\sqrt{2}]$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{2}{3}$,+∞) | B. | [$\frac{2}{3}$,1] | C. | [1,+∞) | D. | [0,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題

| A. | $\frac{1}{6}$ | B. | $\frac{5}{6}$ | C. | $\frac{1}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com