
分析 (1)利用三角函數恒等變換的應用化簡函數解析式可得g(x)=2sin(2x+$\frac{π}{6}$)+m+1,由x的范圍利用正弦函數的圖象可求$g(x)_{max}^{\;}=3+m=6$,即可解得m的值.
(2)由(1)可得:$g(x)=2sin(2x+\frac{π}{6})+4$,利用已知及正弦函數的圖象可求g(x)的最小值,由$2x+\frac{π}{6}=-\frac{π}{2}+2kπ$,解得相應x的取值集合.
(3)利用誘導公式可求g(-x)=$2sin(2x+\frac{5}{6}π)+4$,令$2kπ-\frac{π}{2}≤2x+\frac{5}{6}π≤2kπ+\frac{π}{2}$,可求單調遞增區間.
解答 (本題滿分為12分)
解:(1)∵$g(x)=2\sqrt{3}sinx•cosx+2{cos^2}x+m$=$\sqrt{3}$sin2x+cos2x+m+1=2sin(2x+$\frac{π}{6}$)+m+1,
∵$x∈[0,\frac{π}{2}]$,可得:$-\frac{1}{2}≤sin(2x+\frac{π}{6})≤1$,
∴$g(x)_{max}^{\;}=3+m=6$,
∴m=3.…(4分)
(2)由(1)可得:$g(x)=2sin(2x+\frac{π}{6})+4$,
當x∈R時,g(x)最小值為2,此時$2x+\frac{π}{6}=-\frac{π}{2}+2kπ$,即$x=-\frac{π}{3}+kπ(k∈Z)$取得最小值,
∴x的取值集合為:$\{x\left|{x=-\frac{π}{3}+kπ,k∈Z}\right.\}$.…(8分)
(3)$g(-x)=2sin(-2x+\frac{π}{6})+4$=$2sin(2x+\frac{5}{6}π)+4$,
由$2kπ-\frac{π}{2}≤2x+\frac{5}{6}π≤2kπ+\frac{π}{2}$,可得:$kπ-\frac{2}{3}π≤x≤kπ-\frac{π}{6}$,
∴增區間為:$[kπ-\frac{2}{3}π,kπ-\frac{π}{6}](k∈Z)$.…(12分)
點評 本題主要考查了三角函數恒等變換的應用,正弦函數的圖象和性質,考查了轉化思想和數形結合思想的應用,屬于基礎題.


 科學實驗活動冊系列答案
科學實驗活動冊系列答案科目:高中數學 來源: 題型:解答題
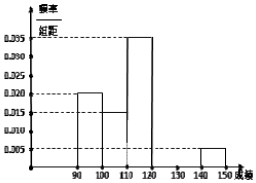 某校高三數學競賽初賽考試結束后,對考生成績進行統計(考生成績均不低于90分,滿分150分),將成績按如下方式分為六組,第一組.如圖為其頻率分布直方圖的一部分,若第四、五、六組的人數依次成等差數列,且第六組有4人.
某校高三數學競賽初賽考試結束后,對考生成績進行統計(考生成績均不低于90分,滿分150分),將成績按如下方式分為六組,第一組.如圖為其頻率分布直方圖的一部分,若第四、五、六組的人數依次成等差數列,且第六組有4人.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{4}{63}$ | B. | $\frac{1}{16}$ | C. | $\frac{3}{63}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 命題“若x2=1,則x=1的否命題為:“若x2=1,則x≠1” | |
| B. | “m=1”是“直線x-my=0和直線x+my=0互相垂直”的充要條件 | |
| C. | 命題“?x0∈R,使得x02+x0+1<0”的否定是:“?x∈R,均有x2+x+1<0” | |
| D. | 命題“已知A,B為一個三角形兩內角,若A=B,則sinA=sinB”的否命題為真命題 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com