
分析 根據函數f(2x)的定義域求出f(x)的定義域,
再由此求出f($\sqrt{{x}^{2}-1}$)的定義域.
解答 解:函數f(2x)的定義域為(1,2),
∴x∈(1,2),∴2x∈(2,4),
∴f(x)的定義域是(2,4);
令2<$\sqrt{{x}^{2}-1}$<4,
得4<x2-1<16,
即5<x2<17,
解得-$\sqrt{17}$<x<-$\sqrt{5}$或$\sqrt{5}$<x<$\sqrt{17}$,
∴f($\sqrt{{x}^{2}-1}$)的定義域為(-$\sqrt{17}$,-$\sqrt{5}$)∪($\sqrt{5}$,$\sqrt{17}$).
故答案為:$({-\sqrt{17},-\sqrt{5}})∪({\sqrt{5},\sqrt{17}})$.
點評 本題考查了函數的定義域及其求法,是基礎題.
①給出f(x)的定義域為[a,b],f[g(x)]的定義域,就是不等式a≤g(x)≤b得x得取值集合,
②給出f[g(x)]的定義域為[a,b],求解f(x)的定義域,就是在x∈[a,b]內的g(x)的值域.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
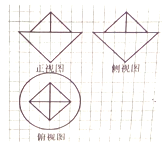 如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,則該幾何體的表面積為( )
如圖,網格紙上小正方形的邊長為1,粗實線畫出的是某幾何體的三視圖,則該幾何體的表面積為( )| A. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$ | B. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$-8 | C. | 9($\sqrt{3}$+2)π+4$\sqrt{3}$ | D. | 9($\sqrt{2}$+1)π+8$\sqrt{3}$-8 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 若a<-1,則x+a<1nx | B. | 若a≥-1,則x+a<1nx | ||
| C. | 若a<-1,則x+a≥1nx | D. | 若a≥-1,則x+a≤1nx |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | b<a<c |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
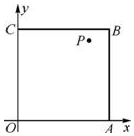 如圖,在邊長為1的正方形OABC內任取一點P(x,y).
如圖,在邊長為1的正方形OABC內任取一點P(x,y).查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com