
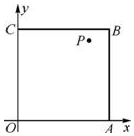
 如圖,在邊長為1的正方形OABC內(nèi)任取一點P(x,y).
如圖,在邊長為1的正方形OABC內(nèi)任取一點P(x,y).分析 (1)根據(jù)題意畫出圖形,結(jié)合圖形求出滿足條件的點P所在的區(qū)域面積,利用幾何概型計算所求的概率;
(2)符合條件的點P構(gòu)成的區(qū)域是圓x2+y2=1在第一象限所圍的平面區(qū)域,利用幾何概型計算所求的概率.
解答 解:(1)如圖所示,取線段BC,AO的中點E,F(xiàn),連接EF,
則當點P在線段EF上時,S△APB=$\frac{1}{4}$,
∴滿足條件的點P所在的區(qū)域為矩形OFEC(陰影部分);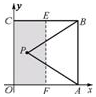
故所求概率為P=$\frac{{S}_{矩形OFEC}}{{S}_{正方形OABC}}$=$\frac{1}{2}$;
(2)所有的點P構(gòu)成正方形區(qū)域D,若點P到原點距離小于1,
則$\left\{\begin{array}{l}{0<x<1}\\{0<y<1}\\{{x}^{2}{+y}^{2}<1}\end{array}\right.$,
所以符合條件的點P構(gòu)成的區(qū)域是
圓x2+y2=1在第一象限所圍的平面區(qū)域如圖中陰影部分,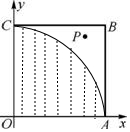
所以點P到原點距離小于1的概率為P=$\frac{\frac{1}{4}•π{•1}^{2}}{{1}^{2}}$=$\frac{π}{4}$.
點評 本題考查了幾何概型的計算問題,關(guān)鍵是正確計算出陰影部分的面積,是基礎(chǔ)題.


科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | y=±$\frac{2}{3}$x | B. | y=±$\frac{1}{6}$x | C. | y=±$\frac{3}{2}$x | D. | y=±6x |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
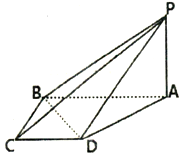 如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,四邊形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.
如圖,在四棱錐P-ABCD中,PA⊥底面ABCD,四邊形ABCD是直角梯形,AB⊥BC,AB∥CD,AB=2BC=2CD=2,PA=1.查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com