
| A. | $\frac{3}{5}$ | B. | $\frac{5}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{5}{4}$ |
分析 求出方程的根,然后利用誘導公式化簡所求的表達式,求解即可.
解答 解:方程5x2-7x-6=0的兩根為x1=-$\frac{3}{5}$,
x2=2.則sinα=-$\frac{3}{5}$,
$\frac{sin(-α-\frac{3π}{2})sin(\frac{3π}{2}-α)tan^2(2π-α)}{cos(\frac{π}{2}-α)cos(\frac{π}{2}+α)sin(π+α)}$=$\frac{-cosαcosαta{n}^{2}α}{sinαsinαsinα}$=-$\frac{1}{sinα}$=$\frac{5}{3}$.
故選:B.
點評 本題考查三角函數化簡求值,誘導公式以及方程的應用,考查函數與方程思想以及計算能力.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 3 | B. | 2 | C. | 9 | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
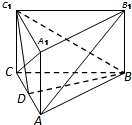 如圖,在正三棱柱(側棱垂直于底面,且底面是正三角形)ABC-A1B1C1中,D是AC邊的中點.
如圖,在正三棱柱(側棱垂直于底面,且底面是正三角形)ABC-A1B1C1中,D是AC邊的中點.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com