
| A. | $\overrightarrow{{a_{10}}}$ | B. | $\overrightarrow{{a_{11}}}$ | C. | $\overrightarrow{{a_{20}}}$ | D. | $\overrightarrow{{a_{21}}}$ |
分析 可設每一項與前一項的差都等于向量$\overrightarrowp9vv5xb5$,運用類似等差數列的通項和求和公式,計算可得$\overrightarrow{{S}_{21}}$=$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+$…+$\overrightarrow{{a}_{21}}$=21($\overrightarrow{{a}_{1}}$+10$\overrightarrowp9vv5xb5$)=21$\overrightarrow{{a}_{11}}$,再由向量共線定理,即可得到所求結論.
解答 解:由新定義可設每一項與前一項的差都等于向量$\overrightarrowp9vv5xb5$,
$\overrightarrow{{S}_{21}}$=$\overrightarrow{{a}_{1}}+\overrightarrow{{a}_{2}}+$…+$\overrightarrow{{a}_{21}}$
=$\overrightarrow{{a}_{1}}+(\overrightarrow{{a}_{1}}+\overrightarrowp9vv5xb5)+…+(\overrightarrow{{a}_{1}}+20\overrightarrowp9vv5xb5)$
=21$\overrightarrow{{a}_{1}}$+$\frac{1}{2}(1+20)•20\overrightarrowp9vv5xb5$
=21($\overrightarrow{{a}_{1}}+10\overrightarrowp9vv5xb5$)
=21$\overrightarrow{{a}_{11}}$,
∴一定平行$\overrightarrow{{S}_{21}}$的向量是$\overrightarrow{{a}_{11}}$.
故選:B.
點評 本題考查新定義:等差向量列的理解和運用,考查類比的思想方法和向量共線定理的運用,屬于中檔題.


 名校名師培優作業本加核心試卷系列答案
名校名師培優作業本加核心試卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 8 | B. | 2 | C. | -2 | D. | 50 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
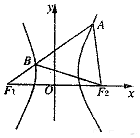 如圖,F1,F2分別是雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦點,過F1的直線l與雙曲線分別交于點A,B,且A(1,$\sqrt{3}$),若△ABF2為等邊三角形,則△BF1F2的面積為( )
如圖,F1,F2分別是雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦點,過F1的直線l與雙曲線分別交于點A,B,且A(1,$\sqrt{3}$),若△ABF2為等邊三角形,則△BF1F2的面積為( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
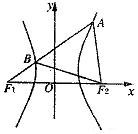 如圖,F1,F2分別是雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦點,過F1的直線l與雙曲線分別交于點A,B,若△ABF2為等邊三角形,則雙曲線的漸近線的斜率為( )
如圖,F1,F2分別是雙曲線$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的左、右焦點,過F1的直線l與雙曲線分別交于點A,B,若△ABF2為等邊三角形,則雙曲線的漸近線的斜率為( )| A. | ±$\sqrt{3}$ | B. | ±2 | C. | $±\sqrt{6}$ | D. | ±$\sqrt{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com