
分析 (I)由已知中側面積和底面積的單位建造成本,結合圓柱體的側面積及底面積公式,根據該蓄水池的總建造成本為10800π元,構造方程整理后,可將V表示成r的函數,進而根據實際中半徑與高為正數,得到函數的定義域;
(Ⅱ)根據(I)中函數的定義值及解析式,利用導數法,可確定函數的單調性,根據單調性,可得函數的最大值點.
解答 解:(Ⅰ)∵蓄水池的側面積的建造成本為100•πrh元,
底面積成本為100πr2元,
∴蓄水池的總建造成本為100•πrh+100πr2元
即100•πrh+100πr2=10800π,
∴h=$\frac{1}{r}$(108-r2)
∴V(r)=πr2h=πr2•$\frac{1}{r}$(108-r2)=π(108r-r3)
又由r>0,h>0可得0<r<6$\sqrt{3}$
故函數V(r)的定義域為(0,6$\sqrt{3}$)
(Ⅱ)由(Ⅰ)中V(r)=π(108r-r3),(0<r<6$\sqrt{3}$)
可得V′(r)=π(108-3r2),(0<r<6$\sqrt{3}$)
∵令V′(r)=π(108-3r2)=0,則r=6
∴當r∈(0,6)時,V′(r)>0,函數V(r)為增函數
當r∈(6,6$\sqrt{3}$)時,V′(r)<0,函數V(r)為減函數
且當r=6,h=12時該蓄水池的體積最大
點評 本題考查的知識點是函數模型的應用,其中(Ⅰ)的關鍵是根據已知,求出函數的解析式及定義域,(Ⅱ)的關鍵是利用導數分析出函數的單調性及最值點.


科目:高中數學 來源: 題型:選擇題
| A. | (0,$\frac{1}{2}$) | B. | (0,1) | C. | ($\frac{1}{2}$,1) | D. | (0,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
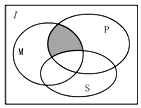
| A. | (M∩P)∪S | B. | (M∩P)∩S | C. | (M∩P)∩(∁IS) | D. | (M∩P)∪(∁IS) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 4 | B. | 2 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com