
分析 (Ⅰ)消去參數t,求得直線l的普通方程,根據x=ρcosθ、y=ρsinθ,求得曲線C的直角坐標方程,聯立方程組求出M、N的直角坐標方程,在轉化為極坐標;
(Ⅱ)設M,N對應的參數分別為t1,t2,${t_1}+{t_2}=4a+2\sqrt{3}>0$,${t_1}{t_2}=4{a^2}>0$即可.
解答 解:(Ⅰ)∵$\left\{\begin{array}{l}x=-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$(t為參數)消去參數t,求得直線l的普通方程$\sqrt{3}x+y=0$
根據x=ρcosθ、y=ρsinθ,求得曲線C的直角坐標方程為x2=y,…(3分)
∴$\left\{\begin{array}{l}{x^2}=y\\ \sqrt{3}x+y=0\end{array}\right.$解得$\left\{\begin{array}{l}x=0\\ y=0\end{array}\right.$或$\left\{\begin{array}{l}x=-\sqrt{3}\\ y=3\end{array}\right.$
∴M,N兩點的極坐標分別為$(2\sqrt{3},\;\frac{2π}{3})$、(0,0)…(6分)
(Ⅱ)點P(a,0)顯然在直線l上,
把$\left\{\begin{array}{l}x=a-\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$(a≥0,t為參數)代入x2=y并化簡,得${t^2}-(4a+2\sqrt{3})t+4{a^2}=0$.
設M,N對應的參數分別為t1,t2,
∵a>0
∴${t_1}+{t_2}=4a+2\sqrt{3}>0$,${t_1}{t_2}=4{a^2}>0$
∴t1>0,t2>0
∴$|PM|+|PN|={t_1}+{t_2}=4a+2\sqrt{3}=8+2\sqrt{3}$
∴a=2.…(12分)
點評 本題考查了極坐標方程、參數方程、普通方程的轉化,及直線的參數方程中參數的含義,屬于基礎題.


科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {5,7} | B. | {2,4} | C. | {2,4,8} | D. | {1,3,5,6,7} |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | y=1 | B. | y=$\frac{(\sqrt{x})^{2}}{x}$ | C. | y=$\frac{x}{x}$ | D. | y=$\frac{|x|+1}{|x|+1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
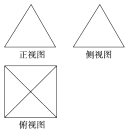 一個幾何體的三視圖如圖所示,正視圖和側視圖都是等邊三角形,且該幾何體的四個點在空間直角坐標系O-xyz中的坐標分別是(0,0,0),(2,0,0),(0,2,0),則第五個頂點的坐標可能為( )
一個幾何體的三視圖如圖所示,正視圖和側視圖都是等邊三角形,且該幾何體的四個點在空間直角坐標系O-xyz中的坐標分別是(0,0,0),(2,0,0),(0,2,0),則第五個頂點的坐標可能為( )| A. | (1,1,1) | B. | (1,1,$\sqrt{2}$) | C. | (1,1,$\sqrt{3}$) | D. | (2,2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ¬p為:?x∈(1,+∞),2x-1-1≤0 | B. | ¬p為:?x∈(1,+∞),2x-1-1<0 | ||
| C. | ¬p為:?x∈(-∞,1],2x-1-1>0 | D. | ¬p是假命題 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com