Question

【題目】已知函數f（x）=4cosωxsin（ωx+ ）（ω＞0）的最小正周期為π．
（1）求ω的值；
（2）討論f（x）在區間[0， ]上的單調性；
（3）當x∈[0， ]時，關于x的方程f（x）=a 恰有兩個不同的解，求實數a的取值范圍．

Answer 1

【答案】
（1）解：f（x）=4cosωxsin（ωx+ ）

=2 sinωxcosωx+2 cos2ωx，

= （sin 2ωx+cos 2ωx）+ ，

=2sin（2ωx+ ）+ ，

因為f（x）的最小正周期為π，且ω＞0，從而有 =π，

故ω=1

（2）解：由（1）知，f（x）=2sin（2x+ ）+ ．若0≤x≤ ，則 ≤2x+ ≤ ．

當 ≤2x+ ≤ ，即0≤x≤ 時，f（x）單調遞增；

當 ≤2x+ ≤ ，即 ≤x≤ 時，f（x）單調遞減．

綜上可知，f（x）在區間[0， ]上單調遞增，在區間[ ， ]上單調遞減

（3）解：x∈[0， ]時，關于x的方程f（x）=a 恰有兩個不同的解，

即y=a與函數在[0， ]上，與f（x）=2sin（2x+ ）+ 由兩個交點，

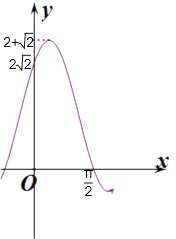
由函數圖象可知：a∈[2 ，2+ ），

實數a的取值范圍[2 ，2+ ）

【解析】（1）由兩角和的正弦公式及輔助角公式化簡f（x），根據周期公式即可求得ω的值；（2）由（1）求得f（x）的解析式，根據正弦函數圖象及性質即可判斷函數區間[0， ]上的單調性；（3）由題意可知y=a與函數在[0， ]上，與f（x）=2sin（2x+ ）+ 由兩個交點，根據函數圖象即可求得實數a的取值范圍．