【題目】某微信群中有甲、乙、丙、丁、戊五個人玩搶紅包游戲，現有4個紅包，每人最多搶一個，且紅包被全部搶完，4個紅包中有2個6元，1個8元，1個10元（紅包中金額相同視為相同紅包），則甲、乙都搶到紅包的情況有（ ）
A. 18種 B. 24種 C. 36種 D. 48種
同步練習河南大學出版社系列答案
同步練習西南師范大學出版社系列答案
補充習題江蘇系列答案
學練快車道口算心算速算天天練系列答案科目：高中數學 來源： 題型：
【題目】某車間共有
名工人,隨機抽取6名,他們某日加工零件個數的莖葉圖如圖所示,其中莖為十位數,葉為個位數.
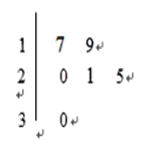
(Ⅰ) 根據莖葉圖計算樣本均值;
(Ⅱ) 日加工零件個數大于樣本均值的工人為優秀工人,根據莖葉圖推斷該車間
名工人中有幾名優秀工人;
(Ⅲ) 從該車間
名工人中,任取2人,求恰有1名優秀工人的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（
且
為常數）．
（1）當
時，討論函數
在
的單調性；
（2）設
可求導數，且它的導函數
仍可求導數，則
再次求導所得函數稱為原函數
的二階函數，記為
，利用二階導函數可以判斷一個函數的凹凸性．一個二階可導的函數在區間
上是凸函數的充要條件是這個函數在
的二階導函數非負．
若
在
不是凸函數，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的焦點
、
在
軸上，且橢圓
經過
，過點
的直線
與
交于點
，與拋物線
： 
交于
、
兩點，當直線
過
時
的周長為
．
（Ⅰ）求
的值和
的方程；
（Ⅱ）以線段
為直徑的圓是否經過
上一定點，若經過一定點求出定點坐標，否則說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，∠ADB=60°，E、F分別是AC、AD上的動點，且
（1）求證：不論
為何值，總有平面BEF⊥平面ABC；
（2）當λ為何值時，平面BEF⊥平面ACD ?
查看答案和解析>>
科目：高中數學 來源： 題型：
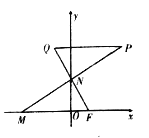
【題目】已知點
，動點
， 
分別在
軸， 
軸上運動， 
， 
為平面上一點， 
，過點
作
平行于
軸交
的延長線于點
.
（Ⅰ）求點
的軌跡曲線
的方程；
（Ⅱ）過
點作
軸的垂線
，平行于
軸的兩條直線
， 
分別交曲線
于
， 
兩點（直線
不過
），交
于
， 
兩點.若線段
中點的軌跡方程為
，求
與
的面積之比.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=4cosωxsin（ωx+ 
）（ω＞0）的最小正周期為π．
（1）求ω的值；
（2）討論f（x）在區間[0， 
]上的單調性；
（3）當x∈[0， ]時，關于x的方程f（x）=a 恰有兩個不同的解，求實數a的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
