
【題目】已知等差數列{an}的公差d>0.設{an}的前n項和為Sn,a1=1,S2·S3=36.
(1)求d及Sn;
(2)求m,k(m,k∈N*)的值,使得am+am+1+am+2+…+am+k=65.
【答案】(1)Snn2;(2) 當m=5,k=4時,am+am+1+…+am+k=65.
【解析】試題分析:(1)已知數列前N項和的關系求通項化為基本量(2a1+d)·(3a1+3d)=36;已知首項的值,可以求得公差,進而求出通項;(2)am+am+1+…+am+k=Sm+k-Sm-1=65,有第一問求出前N項和公式代入即可,在根據k、m是正整數求得值;
(1)∵S2·S3=36,a1=1,
∴(2a1+d)·(3a1+3d)=36, 即d2+3d-10=0,
∴d=2或d=-5. ∵d>0,∴d=2,
∴an為1為首項,2為公差的等差數列,
∴Sn=n+![]() ×2=n2.
×2=n2.
(2)∵am+am+1+…+am+k=65,
∴Sm+k-Sm-1=65.
由(1)得(m+k)2-(m-1)2=65,
即2mk+k2+2m-1=65, 2m(k+1)+k2-1=65,
即(k+1)(2m+k-1)=65=5×13,
∵k、m∈N+,∴2m+k-1>k+1,
∴![]() 解之得
解之得![]() =5,k=4.
=5,k=4.
∴當m=5,k=4時,am+am+1+…+am+k=65.


科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 且
且![]() 為常數).
為常數).
(1)當![]() 時,討論函數
時,討論函數![]() 在
在![]() 的單調性;
的單調性;
(2)設![]() 可求導數,且它的導函數
可求導數,且它的導函數![]() 仍可求導數,則
仍可求導數,則![]() 再次求導所得函數稱為原函數
再次求導所得函數稱為原函數![]() 的二階函數,記為
的二階函數,記為![]() ,利用二階導函數可以判斷一個函數的凹凸性.一個二階可導的函數在區間
,利用二階導函數可以判斷一個函數的凹凸性.一個二階可導的函數在區間![]() 上是凸函數的充要條件是這個函數在
上是凸函數的充要條件是這個函數在![]() 的二階導函數非負.
的二階導函數非負.
若![]() 在
在![]() 不是凸函數,求
不是凸函數,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分別為AC、DC的中點. 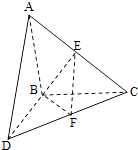
(1)求證:EF⊥BC;
(2)求二面角E﹣BF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=Asin(ωx+φ)(A,ω>0,﹣π<φ<π)在一個周期內的圖象如圖所示. 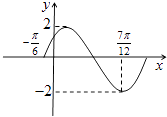
(1)求f(x)的表達式;
(2)在△ABC中,f(C+ ![]() )=﹣1且
)=﹣1且 ![]() <0,求角C.
<0,求角C.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=4cosωxsin(ωx+ ![]() )(ω>0)的最小正周期為π.
)(ω>0)的最小正周期為π.
(1)求ω的值;
(2)討論f(x)在區間[0, ![]() ]上的單調性;
]上的單調性;
(3)當x∈[0, ![]() ]時,關于x的方程f(x)=a 恰有兩個不同的解,求實數a的取值范圍.
]時,關于x的方程f(x)=a 恰有兩個不同的解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2sinx(sinx+ ![]() cosx)﹣1(其中x∈R),求:
cosx)﹣1(其中x∈R),求:
(1)函數f(x)的最小正周期;
(2)函數f(x)的單調減區間;
(3)函數f(x)圖象的對稱軸和對稱中心.
查看答案和解析>>
科目:高中數學 來源: 題型:
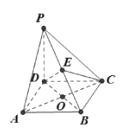
【題目】如圖,在四棱錐![]() 中,
中, ![]() 平面
平面![]() ,四邊形
,四邊形![]() 是菱形,
是菱形, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 交于點
交于點![]() ,
, ![]() 是
是![]() 上任意一點.
上任意一點.
(1)求證: ![]() ;
;
(2)已知二面角![]() 的余弦值為
的余弦值為![]() ,若
,若![]() 為
為![]() 的中點,求
的中點,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com