
分析 根據題意,由函數g(x)的解析式分析可得g(x)為偶函數,且在[0,+∞)上為增函數;由此可以將g(x-1)>g(3x+1)轉化為|x-1|>|3x+1|,解可得x的取值范圍,即可得答案.
解答 解:根據題意,對于函數$g(x)={e^{1+{x^2}}}-\frac{1}{{1+{x^2}}}+|x|$,
$g(-x)={e^{1+{x^2}}}-\frac{1}{{1+{x^2}}}+|-x|$=g(x),則g(x)為偶函數.
分析易知g(x)在[0,+∞)上為增函數.
則g(x-1)>g(3x+1)?g(|x-1|)>g(|3x+1|)?|x-1|>|3x+1|,
解可得-1<x<0;
即x的取值范圍為(-1,0);
故答案為:(-1,0).
點評 本題考查函數的奇偶性與單調性的綜合應用,關鍵是分析函數的奇偶性與單調性.


 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
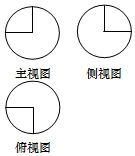 如圖,某幾何體的三視圖是三個半徑相等的圓及每個圓中兩條相互垂直的半徑,若該幾何體的體積是$\frac{28π}{3}$,則三視圖中圓的半徑為( )
如圖,某幾何體的三視圖是三個半徑相等的圓及每個圓中兩條相互垂直的半徑,若該幾何體的體積是$\frac{28π}{3}$,則三視圖中圓的半徑為( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 2 | B. | $\sqrt{2}$ | C. | $-\sqrt{2}$ | D. | -2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{5}{8}$ | B. | $-\frac{7}{8}$ | C. | $-\frac{5}{8}$ | D. | $\frac{7}{8}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
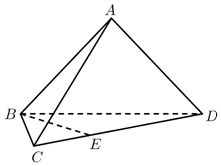 如圖,在三棱錐A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,點E在CD上,DE=2EC.
如圖,在三棱錐A-BCD中,平面ABD⊥平面BCD,AB=AD,∠CBD=60°,BD=2BC=4,點E在CD上,DE=2EC.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com