Question

14．已知$|{\overrightarrow{OA}}|=2$，$|{\overrightarrow{OB}}|=2$，且向量$\overrightarrow{OA}$與$\overrightarrow{OB}$的夾角為120°，又$|{\overrightarrow{PO}}|=\sqrt{3}$，則$\overrightarrow{AP}•\overrightarrow{BP}$的取值范圍是$[{1-2\sqrt{3}，1+2\sqrt{3}}]$．

Answer 1

分析 利用平面向量的運算，將$\overrightarrow{AP}•\overrightarrow{BP}$寫成（$\overrightarrow{OP}-\overrightarrow{OA}$）•（$\overrightarrow{OP}-\overrightarrow{OB}$）=${\overrightarrow{OP}}^{2}+\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OP}•（\overrightarrow{OA}+\overrightarrow{OB}）$=1-$\overrightarrow{OP}•（\overrightarrow{OA}+\overrightarrow{OB}）$，利用其幾何意義求最值．

解答 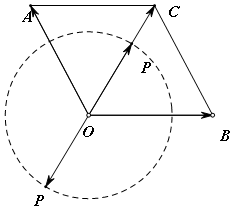解：由已知得到$\overrightarrow{AP}•\overrightarrow{BP}$=（$\overrightarrow{OP}-\overrightarrow{OA}$）•（$\overrightarrow{OP}-\overrightarrow{OB}$）=${\overrightarrow{OP}}^{2}+\overrightarrow{OA}•\overrightarrow{OB}-\overrightarrow{OP}•（\overrightarrow{OA}+\overrightarrow{OB}）$=1-$\overrightarrow{OP}•（\overrightarrow{OA}+\overrightarrow{OB}）$，
因為$|{\overrightarrow{OA}}|=2$，$|{\overrightarrow{OB}}|=2$，且向量$\overrightarrow{OA}$與$\overrightarrow{OB}$的夾角為120°，所以$\overrightarrow{OA}+\overrightarrow{OB}$表示以$\overrightarrow{OA}$，$\overrightarrow{OB}$為鄰邊的菱形的對角線對應的向量$\overrightarrow{OC}$，
如圖
所以$\overrightarrow{OP}•\overrightarrow{OC}$的最大值為$|\overrightarrow{OP}||\overrightarrow{OC}|cos0=2\sqrt{3}$．最小值為|$|\overrightarrow{OP}||\overrightarrow{OC}|cosπ=-2\sqrt{3}$，
所以$\overrightarrow{AP}•\overrightarrow{BP}$的取值范圍是[1-2$\sqrt{3}$，1+2$\sqrt{3}$]；
故答案為：[1-2$\sqrt{3}$，1+2$\sqrt{3}$]．

點評 本題考查了平面向量的運算，關鍵是將所求變形，利用其幾何意義求最值．