
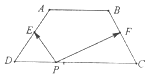
 如圖,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分別為AD與BC的中點,對于常數λ,在梯形ABCD的四條邊上恰好有8個不同的點P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,則實數λ的取值范圍是( )
如圖,梯形ABCD中,AB∥CD,AB=2,CD=4,BC=AD=$\sqrt{5}$,E和F分別為AD與BC的中點,對于常數λ,在梯形ABCD的四條邊上恰好有8個不同的點P,使得$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,則實數λ的取值范圍是( )| A. | (-$\frac{5}{4}$,-$\frac{9}{20}$) | B. | (-$\frac{5}{4}$,$\frac{11}{4}$) | C. | (-$\frac{1}{4}$,$\frac{11}{4}$) | D. | (-$\frac{9}{20}$,-$\frac{1}{4}$) |
分析 建立坐標系,設P的坐標,根據建立坐標系,設P的坐標,根據$\overrightarrow{PE}$$•\overrightarrow{PF}$=λ得到λ關于x的方程,根據P的位置分四種情況討論方程解得情況.
解答  解:以DC所在直線為x軸,DC的中垂線為y軸建立平面直角坐標系
解:以DC所在直線為x軸,DC的中垂線為y軸建立平面直角坐標系
則梯形的高為$\sqrt{5-1}$=2,∴A(-1,2),B(1,2),C(2,0),D(-2,0),∴E(-$\frac{3}{2}$,1),F($\frac{3}{2}$,1).
1)當P在DC上時,設P(x,0)(-2≤x≤2),則$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,1),$\overrightarrow{PF}$=($\frac{3}{2}$,1).
于是$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+1=x2-$\frac{5}{4}$=λ,
∴當λ=-$\frac{5}{4}$時,方程有一解,當-$\frac{5}{4}$<λ≤$\frac{11}{4}$時,λ有兩解;
(2)當P在AB上時,設P(x,2)(-1≤x≤1),則$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,-1),$\overrightarrow{PF}$=($\frac{3}{2}$,-1).
∴$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+1=x2-$\frac{5}{4}$=λ,
∴當λ=-$\frac{5}{4}$時,方程有一解,當-$\frac{5}{4}$<λ≤-$\frac{1}{4}$時,λ有兩解;
(3)當P在AD上時,直線AD方程為y=2x+4,
設P(x,2x+4)(-2<x<-1),則$\overrightarrow{PE}$=(-$\frac{3}{2}$-x,-2x-3),$\overrightarrow{PF}$=($\frac{3}{2}$-x,-2x-3).
于是$\overrightarrow{PE}$$•\overrightarrow{PF}$=(-$\frac{3}{2}$-x)($\frac{3}{2}$-x)+(-2x-3)2=5x2+12x+$\frac{27}{4}$=λ.
∴當λ=-$\frac{9}{20}$或-$\frac{1}{4}$<λ<$\frac{9}{4}$時,方程有一解,當-$\frac{9}{20}$<λ<-$\frac{1}{4}$時,方程有兩解;
(4)當P在CD上時,由對稱性可知當λ=-$\frac{9}{20}$或-$\frac{1}{4}$<λ<$\frac{9}{4}$時,方程有一解,
當-$\frac{9}{20}$<λ<-$\frac{1}{4}$時,方程有兩解;
綜上,若使梯形上有8個不同的點P滿足$\overrightarrow{PE}$•$\overrightarrow{PF}$=λ成立,
則λ的取值范圍是(-$\frac{5}{4}$,$\frac{11}{4}$]∩(-$\frac{5}{4}$,-$\frac{1}{4}$]∩(-$\frac{9}{20}$,-$\frac{1}{4}$)∩(-$\frac{9}{20}$,-$\frac{1}{4}$)=(-$\frac{9}{20}$,-$\frac{1}{4}$).
故選D.
點評 本題考查了平面向量的數量積運算,二次函數與二次方程的關系,分類討論思想,屬于中檔題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
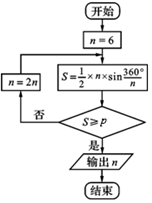 三世紀中期,魏晉時期的數學家劉徽首創割圓術,為計算圓周率建立了嚴密的理論和完善的算法,所謂割圓術,就是用圓內接正多邊形的面積去無限逼近圓面積并以此求取圓周率的方法.按照這樣的思路,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和 3.1416這兩個近似數值.如圖所示是利用劉徽的割圓術設計的程序框圖,若輸出的n=24,則p的值可以是(參考數據:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )
三世紀中期,魏晉時期的數學家劉徽首創割圓術,為計算圓周率建立了嚴密的理論和完善的算法,所謂割圓術,就是用圓內接正多邊形的面積去無限逼近圓面積并以此求取圓周率的方法.按照這樣的思路,劉徽把圓內接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和 3.1416這兩個近似數值.如圖所示是利用劉徽的割圓術設計的程序框圖,若輸出的n=24,則p的值可以是(參考數據:$\sqrt{3}$=1.732,sin15°≈0.2588,sin7.5°≈0.1305,sin3.75°≈0.0654)( )| A. | 2.6 | B. | 3 | C. | 3.1 | D. | 3.14 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
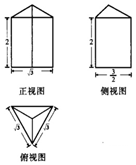 如圖是由正三棱椎與正三棱柱組合而成的幾何體的三視圖,該幾何體的頂點都在半徑為R的球面上,則R=( )
如圖是由正三棱椎與正三棱柱組合而成的幾何體的三視圖,該幾何體的頂點都在半徑為R的球面上,則R=( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{1+\sqrt{2}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com